
【题目】某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
【答案】(1)购买甲种树苗500株,乙种树苗300株(2)320株(3)当选购甲种树苗320株,乙种树苗480株时,总费用最低,为22080元
【解析】
(1)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株,得
株,得
![]() 解得
解得![]()
答:购买甲种树苗500株,乙种树苗300株。
(2)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株,得
株,得
![]() 解得
解得![]()
答:甲种树苗至少购买320株。
(3)设甲种树苗购买![]() 株,购买树苗的费用为
株,购买树苗的费用为![]() 元,
元,
则![]()
∵![]() ∴
∴![]() 随
随![]() 增大而减小 ∴
增大而减小 ∴![]()
当![]() 时,
时,![]() 有最小值,
有最小值,![]() 最小=
最小=![]() 元
元
答:当选购甲种树苗320株,乙种树苗480株时,总费用最低,为22080元。
(1)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株,列方程组求得
株,列方程组求得
(2)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株,列不等式求解
株,列不等式求解
(3)设甲种树苗购买![]() 株,购买树苗的费用为
株,购买树苗的费用为![]() 元,列出关系式,根据函数的性质求出w的最小值.
元,列出关系式,根据函数的性质求出w的最小值.


科目:初中数学 来源: 题型:
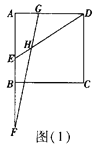
【题目】如图,四边形ABCD为正方形,点E在边 AB上,点F在AB的延长线上,点G在边AD上,且EF= ![]() AB,DG=
AB,DG= ![]() AE,连接DE、FG相交于点H.
AE,连接DE、FG相交于点H.
(1)若![]() ,如图(1),求∠EHF的度数(提示:连接CG,CF);
,如图(1),求∠EHF的度数(提示:连接CG,CF);
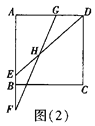
(2)若![]() ,如图(2),求tan∠EHF的值.
,如图(2),求tan∠EHF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
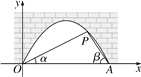
【题目】图中是抛物线型拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α,β,tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少(![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.
(1)如果小张家一个月用电128度,那么这个月应缴纳电费多少元?
(2)如果小张家一个月用电a度![]() ,那么这个月应缴纳电费多少元?(用含a的代数式表示)
,那么这个月应缴纳电费多少元?(用含a的代数式表示)
(3)如果这个月缴纳电费为147.8元,那么小张家这个月用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:|﹣6|﹣7+(﹣3)
(2)计算:﹣32÷3﹣![]() ×(﹣2)3
×(﹣2)3
(3)化简:2(2x2y+x)﹣3(x2y﹣2x)
(4)解方程:5﹣2x=3(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
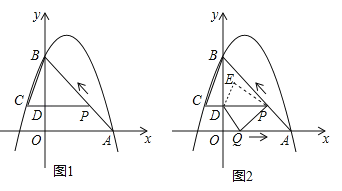
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

查看答案和解析>>
科目:初中数学 来源: 题型:
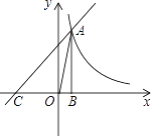
【题目】如图,在直角坐标系中,直线y=x+m与y=![]() 在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
(1)求m的值;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com