
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
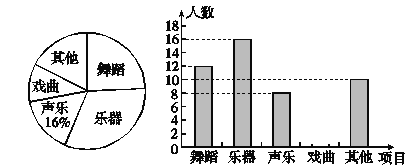
请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了__________名学生;
(2)请将最喜欢活动为 “戏曲”的条形统计图补充完整;
(3)你认为在扇形统计图中,“其他”所在的扇形对应的圆心角的度数是__________°;
(4)若该校共有3100名学生,请你估计全校对“乐器”最喜欢的人数是________人.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为![]() .例如
.例如![]() ,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以
,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以![]() .
.
(1)计算:![]() 和
和![]() ;
;
(2)若![]() 是“相异数”,证明:
是“相异数”,证明:![]() 等于
等于![]() 的各数位上的数字之和.
的各数位上的数字之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E,F在对角线AC上,且AE=CF。
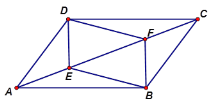
(1)求证:四边形DEBF是平行四边形;
(2)若DE=3,CD=4,∠EDC=90°,当四边形DEBF是菱形时,AE的长为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
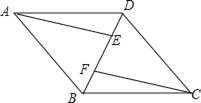
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
小白遇到这样一个问题:
如图,点C是段AB的中点,AD=![]() DB,CD=10,求AB的长.
DB,CD=10,求AB的长.
![]()
小白的思路是:设AB=x,根据“CD=10“列方程,请按照小白的思路完成此问题的解答
用学过的知识或参考小白的方法,解决下面的问题:
已知OC、OD是∠AOB的内部的两条射线,∠AOC═![]() ∠AOB,∠AOD=m∠DOB,∠COD=n(m、n为常数,且m≠
∠AOB,∠AOD=m∠DOB,∠COD=n(m、n为常数,且m≠![]() )
)
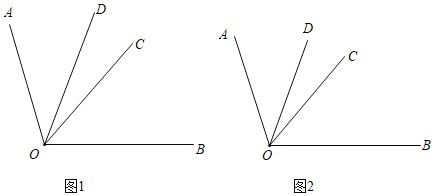
(1)如图1,若m=![]() ,n=22,求∠DOB的度数.
,n=22,求∠DOB的度数.
(2)如图2,若n=14(3﹣2m)求∠DOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
(1)求证:△BCE≌△DCF;
(2)OG与BF有什么数量关系?证明你的结论;
(3)若GE·GB=4-2![]() ,求正方形ABCD的面积.
,求正方形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
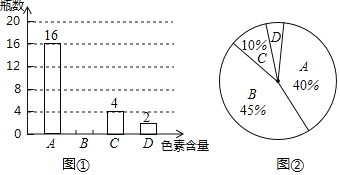
【题目】食品安全关系到我们每个人的身心健康,为了调查市场上某品牌饮料的色素含量是否符合国家标准,工作人员在超市里随机抽取了该品牌饮料进行检验,图①和图②是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图①的条形统计图表示的是抽查的饮料中各种色素含量分布的瓶数,图②的扇形统计图表示的是抽查的饮料中各种色素含量的瓶数占抽查总数的百分比.
请根据以上信息解答以下问题:
(1)本次调查一共抽查了多少瓶饮料?
(2)请将图①条形统计图中色素含量为B的部分补充完整;
(3)图②扇形统计图中色素含量为D的部分的扇形圆心角是多少度?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的饮料共有5000瓶,估计其中不合格的产品约有多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元9世纪,阿拉伯数学家阿尔花拉子米在他的名著《代数学》中用图解一元二次方程,他把一元二次方程![]() 写成
写成![]() 的形式,并将方程左边的
的形式,并将方程左边的![]() 看作是由一个正方形(边长为
看作是由一个正方形(边长为![]() )和两个同样的矩形(一边长为
)和两个同样的矩形(一边长为![]() ,另一边长为
,另一边长为![]() )构成的矩尺形,它的面积为
)构成的矩尺形,它的面积为![]() ,如图所示。于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为:
,如图所示。于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为:![]() ____
____![]() _______ ,整理,得
_______ ,整理,得![]() ,因为
,因为![]() 表示边长,所以
表示边长,所以![]() ___________.
___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com