
【题目】如图,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:①PA=PE;②CE=![]() PD;③BF﹣PD=
PD;③BF﹣PD=![]() BD;④S△PEF=S△ADP,正确的是___(填写所有正确结论的序号)
BD;④S△PEF=S△ADP,正确的是___(填写所有正确结论的序号)
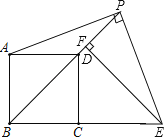
【答案】①②③.
【解析】
①解法一:如图1,作辅助线,构建三角形全等和平行四边形,证明![]() ,得BG=PE,再证明四边形ABGP是平行四边形,可得结论;
,得BG=PE,再证明四边形ABGP是平行四边形,可得结论;
解法二:如图2,连接AE,利用四点共圆证明△APE是等腰直角三角形,可得结论;
②如图3,作辅助线,证明四边形DCGP是平行四边形,可得结论;
③证明四边形OCGF是矩形,可作判断;
④证明![]() ,则
,则![]() ,可作判断.
,可作判断.
①解法一:如图1,在EF上取一点G,使FG=FP,连接BG、PG,
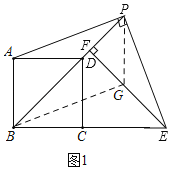
∵EF⊥BP,
∴∠BFE=90°,
∵四边形ABCD是正方形,
∴∠FBC=∠ABD=45°,
∴BF=EF,
在△BFG和△EFP中,
∵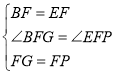 ,
,
∴△BFG≌△EFP(SAS),
∴BG=PE,∠PEF=∠GBF,
∵∠ABD=∠FPG=45°,
∴AB∥PG,
∵AP⊥PE,
∴∠APE=∠APF+∠FPE=∠FPE+∠PEF=90°,
∴∠APF=∠PEF=∠GBF,
∴AP∥BG,
∴四边形ABGP是平行四边形,
∴AP=BG,
∴AP=PE;
解法二:如图2,连接AE,∵∠ABC=∠APE=90°,
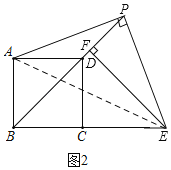
∴A、B、E、P四点共圆,
∴∠EAP=∠PBC=45°,
∵AP⊥PE,
∴∠APE=90°,
∴△APE是等腰直角三角形,
∴AP=PE,
故①正确;
②如图3,连接CG,由①知:PG∥AB,PG=AB,
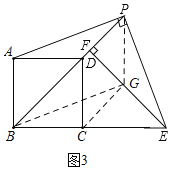
∵AB=CD,AB∥CD,
∴PG∥CD,PG=CD,
∴四边形DCGP是平行四边形,
∴CG=PD,CG∥PD,
∵PD⊥EF,
∴CG⊥EF,即∠CGE=90°,
∵∠CEG=45°,
∴![]() ;
;
故②正确;
③如图4,连接AC交BD于O,由②知:∠CGF=∠GFD=90°,
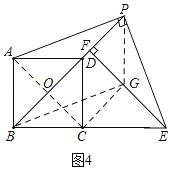
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠COF=90°,
∴四边形OCGF是矩形,
∴CG=OF=PD,
∴![]() ,
,
故③正确;
④如图4中,在△AOP和△PFE中,
∵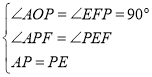 ,
,
∴△AOP≌△PFE(AAS),
∴![]() ,
,
∴![]() ,
,
故④不正确;
本题结论正确的有:①②③,
故答案为:①②③.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,给出下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABF:S四边形CDEF=2:5,其中正确的结论有( )
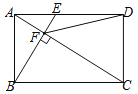
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-2x+1=0.
(1)若方程有两个实数根,求m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2-x1-x2=![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知二次函数![]() .以下四个结论:
.以下四个结论:
①不论![]() 取何值,图象始终过点(
取何值,图象始终过点(![]() ,
,![]() );
);
②当![]() 时,抛物线与
时,抛物线与![]() 轴没有交点:
轴没有交点:
③当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④当![]() 时,抛物线的顶点达到最高位置.
时,抛物线的顶点达到最高位置.
请你分别判断四个结论的真假,并给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是矩形ABCD的边AD延长线上一点,以AM为直径的⊙O交矩形对角线AC于点F,在线段CD上取一点E,连接EF,使EC=EF.

(1)求证:EF是⊙O的切线;
(2)若cos∠CAD=![]() ,AF=6,MD=2,求FC的长.
,AF=6,MD=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有点A(-4,0)、B(0,3)、P(a,-a)三点,线段CD与AB关于点P中心对称,其中A、B的对应点分别为C、D
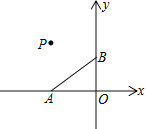
(1) 当a=-4时
① 在图中画出线段CD,保留作图痕迹
② 线段CD向下平移 个单位时,四边形ABCD为菱形
(2) 当a=___________时,四边形ABCD为正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O是△ABC的外接圆,AB是直径,D是⊙O外一点且满足∠DCA=∠B,连接AD.
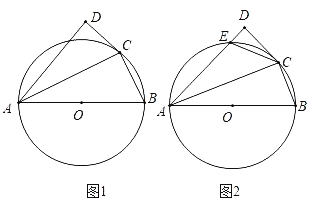
(1)求证:CD是⊙O的切线;
(2)若AD⊥CD,CD=2,AD=4,求直径AB的长;
(3)如图2,当∠DAB=45°时,AD与⊙O交于E点,试写出AC、EC、BC之间的数量关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com