
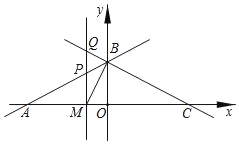
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
【答案】(1)y=﹣![]() x+3;(2)①P(﹣
x+3;(2)①P(﹣![]() ,0);②M(
,0);②M(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)先根据坐标轴上点的特点求出A,B的坐标,进而求出点C坐标,最后用待定系数法即可得出结论;
(2)①设出点M的坐标,利用勾股定理求出BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,最后用勾股定理建立方程求解,即可得出结论;
②设出点M的坐标,进而得出点P,Q坐标,即:得出PQ,最后用面积公式即可得出结论.
解:(1)对于y=![]() x+3,令x=0,y=3,
x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴![]() x+3=0,
x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴![]() ,
,
∴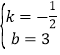 ,
,
∴直线BC的解析式为y=﹣![]() x+3;
x+3;
(2)①设点M(m,0),
∴P(m,![]() m+3),
m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣![]() ,∴P(﹣
,∴P(﹣![]() ,0);
,0);
②设点M(n,0),
∵点P在直线AB:y=![]() x+3上,
x+3上,
∴P(n,![]() n+3),
n+3),
∵点Q在直线BC:y=﹣![]() x+3上,
x+3上,
∴Q(n,﹣![]() n+3),
n+3),
∴PQ=|![]() n+3﹣(﹣
n+3﹣(﹣![]() n+3)|=|n|,
n+3)|=|n|,
∵△PQB的面积为![]() ,
,
∴S△PQB=![]() |n||n|=
|n||n|=![]() n2=
n2=![]() ,
,
∴n=±![]() ,
,
∴M(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
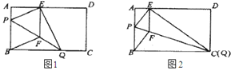
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售每台进价分别为180元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 2台 | 3台 | 1100元 |
第二周 | 4台 | 5台 | 2000元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求甲、乙两种型号的电器的销售单价;
(2)若超市准备用不多于5000元的金额再采购这两种型号的电器共30台,求甲种型号的电器最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电器能否实现利润超过1900元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△OAB的位置如图所示.将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;…依此类推,第9次旋转得到△OA9B9,则顶点A的对应点A9的坐标为_____.
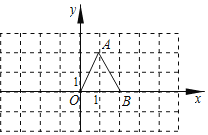
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,…,
,…, ![]() ,则
,则![]() = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com