
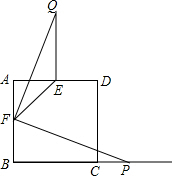
 如图,正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FQ,连接EQ,则EF、EQ、BP三者之间的数量关系为EF=$\sqrt{2}$(BP-EQ)..
如图,正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FQ,连接EQ,则EF、EQ、BP三者之间的数量关系为EF=$\sqrt{2}$(BP-EQ).. 分析 取BC的中点G,连接FG,根据同角的余角相等求出∠1=∠3,然后利用“边角边”证明△FQE和△FPG全等,根据全等三角形对应边相等可得QE=FG,BF=BG,再根据BG+GP=BP等量代换即可得证;
解答 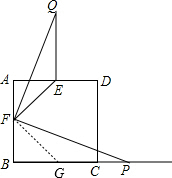 解:如图,取BC的中点G,连接FG,
解:如图,取BC的中点G,连接FG,
∵点E、F、G分别是正方形边AD、AB、BC的中点,
∴△AEF和△BGD是两个全等的等腰直角三角形.
∴EF=FG,∠AFE=∠BFG=45°.
∴∠EFG=90°,即EF⊥FG.
根据旋转的性质,FP=FQ,∠PFQ=90°.
∴∠GFP=∠GFE-∠EFP=90°-∠EFP,
∠EFQ=∠PFQ-∠EFP=90°-∠EFP.
∴∠GFP=∠EFQ.
在△FQE和△FPG中,
∵EF=GF,∠EFQ=∠GFP,FQ=FP,
∴△FQE≌△FPG(SAS).
∴EQ=GP.
∴EF=GF=$\sqrt{2}$GB=$\sqrt{2}$(BP-GP)=$\sqrt{2}$(BP-EQ),
故答案为:EF=$\sqrt{2}$(BP-EQ)..
点评 本题考查了正方形的性质、全等三角形的判定与性质以及旋转的性质.注意在正方形中的特殊三角形的应用,搞清楚正方形中的三角形的三边关系,可有助于提高解题速度和准确率.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
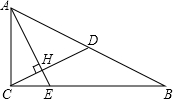 如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
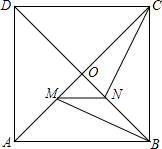 如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.
如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD内接于⊙O,∠A=100°,则劣弧$\widehat{BD}$的度数是( )
如图,四边形ABCD内接于⊙O,∠A=100°,则劣弧$\widehat{BD}$的度数是( )| A. | 80° | B. | 100° | C. | 130° | D. | 160° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com