
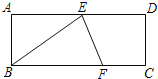
【题目】如图,在矩形ABCD中,E为AD的中点,∠BED的平分线交BC于点F,若AB=3,BC=8,则FC的长度为( )
A. 6B. 5C. 4D. 3
【答案】D
【解析】
根据矩形点的性质可得AD∥BC,AD=BC,再求出AE的长度,再根据勾股定理列式求出BE的长,然后根据角平分线的定义求出∠BEF=∠DEF,根据两直线平行,内错角相等求出∠BFE=∠DEF,再求出BEF=∠BFE,根据等角对等边可得BE=BF,然后根据FC=BC-BF代入数据计算即可得解.
解:在矩形ABCD中,AD∥BC,AD=BC=8,
∵E为AD的中点,
∴AE=![]() AD=
AD=![]() ×8=4,
×8=4,
在Rt△ABE中,![]() ,
,
∵EF是∠BED的角平分线,
∴∠BEF=∠DEF,
∵AD∥BC,
∴∠BFE=∠DEF,
∴BEF=∠BFE,
∴BE=BF,
∴FC=BC-BF=8-5=3.
故选:D.


科目:初中数学 来源: 题型:
【题目】某学校组织了“热爱宪法,捍卫宪法”的知识竞赛,赛后发现所有学生的成绩(总分100分)均不低于50分,为了解本次竞赛的成绩分布情况,随机抽取若干名学生的成绩作为样本进行整理,并绘制了不完整的统计图表,请你根据统计图表解答下列问题.
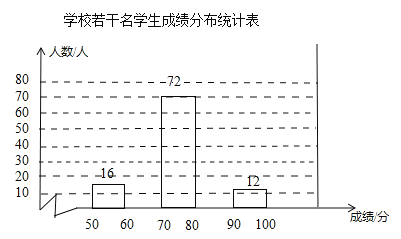
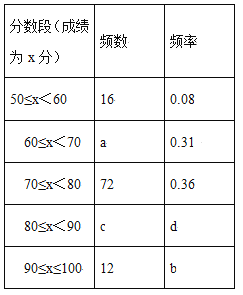
(1)此次抽样调查的样本容量是_________;
(2)写出表中的a=_____,b=______,c=________;
(3)补全学生成绩分布直方图;
(4)比赛按照分数由高到低共设置一、二、三等奖,若有25%的参赛学生能获得一等奖,则一等奖的分数线是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
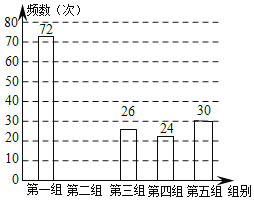
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
组别 | 单次营运里程“x”(千米) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据以上信息,解答下列问题:
(1)表中a= ,样本中“单次营运里程”不超过15千米的频率为 ;
(2)请把频数分布直方图补充完整;
(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
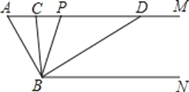
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级开展“社会主义核心价值观”演讲比赛活动,九(1)班、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出5名选手的复赛成绩(满分100分)如图所示.

根据图中数据解决下列问题:
(1)九(1)班复赛成绩的众数是 分,九(2)班复赛成绩的中位数是 分;
(2)请你求出九(1)班和九(2)班复赛的平均成绩和方差,并说明哪个班的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
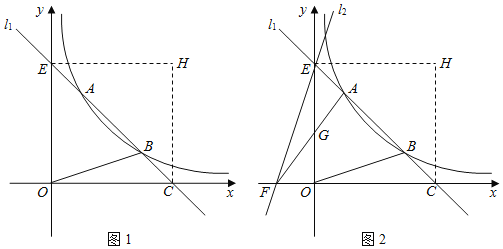
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com