
【题目】已知![]() 是
是![]() 的一条弦,点
的一条弦,点![]() 在
在![]() 上,联结
上,联结![]() 并延长,交弦
并延长,交弦![]() 于点
于点![]() ,且
,且![]() .
.
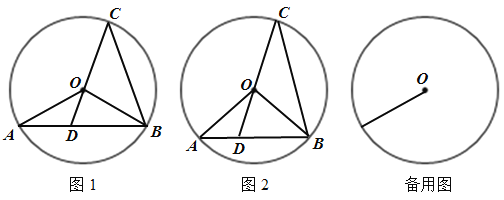
(1)如图1,如果![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,如果![]() ,求
,求![]() 的值;
的值;
(3)延长线段![]() 交弦
交弦![]() 于点
于点![]() ,如果
,如果![]() 是等腰三角形,且
是等腰三角形,且![]() 的半径长等于
的半径长等于![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]() 和
和![]()
【解析】
(1)由题意利用弦心距即可求证结果,
(2)此题关键先求出AO,做辅助线构造特殊三角形,并求证出∠AOD,再根据平行线分线段成比例求出比值即可,
(3)分情况讨论两种情况:OE=BE时或OB=BE时两种情况,利用三角形相似即△COE![]() △CBO找到相似比,利用相似比求解即可.
△CBO找到相似比,利用相似比求解即可.
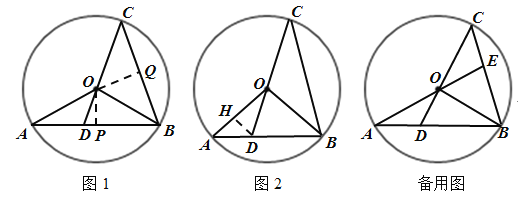
(1)过点O作OP⊥AB,垂足为点P;OQ⊥BC,垂足为点Q,
∵BO平分∠ABC,
∴OP=OQ,
∵OP,OQ分别是弦AB、BC 的弦心距,
∴AB= BC;
(2)∵OA=OB,
∴∠A=∠OBD,
∵CD=CB,
∴∠CDB =∠CBD,
∴∠A+∠AOD =∠CBO +∠OBD,
∴∠AOD =∠CBO,
∵OC=OB,
∴∠C =∠CBO,
∴∠DOB =∠C +∠CBO = 2∠CBO = 2∠AOD,
∵AO⊥OB,
∴∠ AOB =∠AOD +∠BOD =3∠AOD = 90°,
∴∠AOD=30°,
过点D作DH⊥AO,垂足为点H,
∴∠AHD=∠DHO=90°,
∴tan∠AOD =![]() =
=![]() ,
,
∵∠AHD=∠AOB=90°,
∴HD‖OB,
∴![]() ,
,
∵OA=OB,
∴HD=AH,
∵HD‖OB,
∴![]() ;
;
(3)∵∠C=∠CBO,
∴∠OEB =∠C+∠COE >∠CBO,
∴OE≠OB;
若OB = EB =2时,
∵∠C=∠C,∠COE =∠AOD =∠CBO,
∴△COE![]() △CBO,
△CBO,
∴![]() ,
,
∴![]() ,
,
∴![]() -2BC -4=0,
-2BC -4=0,
∴BC =![]() +1 (舍去)或BC =
+1 (舍去)或BC =![]() +1,
+1,
∴BC =![]() +1;
+1;
若OE = EB时,
∵∠EOB =∠CBO,
∵∠OEB =∠C+∠COE =2∠C =2∠CBO且∠OEB +∠CBO +∠EOB = 180°,
∴4∠CBO=180°,∠CBO=45°,
∴∠OEB=90°,
∴cos∠CBO=![]() ,
,
∵OB=2,
∴EB =![]() ,
,
∵OE过圆心,OE⊥BC,
∴BC =2EB =2![]() .
.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
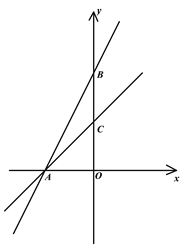
【题目】如图,在平面直角坐标系中,直线AB![]() 与x轴,y轴,交于A、B两点,点C是BO的中点且
与x轴,y轴,交于A、B两点,点C是BO的中点且![]()
(1)求直线AC的解析式;
(2)若点M是直线AC的一点,当![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
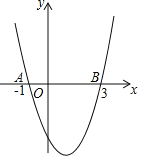
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CD是AB边上的中线,点E在边AC上(不与A,C重合),且BE=CD.设![]() =k,若符合条件的点E有两个,则k的取值范围是_____.
=k,若符合条件的点E有两个,则k的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“联络四边形”,已知圆的半径长为![]() ,这个圆的一个联络四边形是边长为
,这个圆的一个联络四边形是边长为![]() 的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.
的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
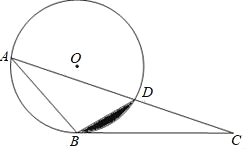
【题目】如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)证明BC与⊙O相切;
(2)若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
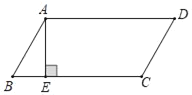
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D,E分别是边
,点D,E分别是边![]() ,
,![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点C按逆时针方向旋转,记旋转角为α.
绕点C按逆时针方向旋转,记旋转角为α.
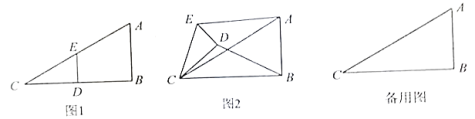
(1)问题发现
①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;
;
(2)拓展探究
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
当![]() 旋转至
旋转至![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com