
【题目】如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“联络四边形”,已知圆的半径长为![]() ,这个圆的一个联络四边形是边长为
,这个圆的一个联络四边形是边长为![]() 的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.
的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.
【答案】1
【解析】
此题应根据题意先找到圆心位置,再根据圆心位置求出不在圆上的顶点到该圆圆心的距离即可.

根据题意作图可分两种情况:1如图:作![]() , BC=
, BC=![]() ,BO=5,
,BO=5,
∵A,B,C在圆O上,
∴BP=![]() (垂径定理),
(垂径定理),
又![]() ,
,
∴OP=![]() =
= ![]() =
=![]() ;
;
因为ABCD是菱形,
∴AC![]() BD,即∠BQC=90°,
BD,即∠BQC=90°,
在△BOP与△BQC中,
![]() ,
,
∴△BOP![]() △BQC,
△BQC,
∴![]() ,
,
即![]() ,
,
∴BQ=2,
∵BQ>BO,
∴此情况不符合题意,舍去;
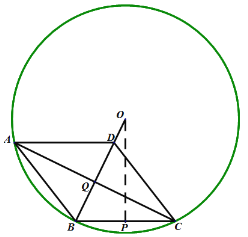
2,如图,同理可得OP=![]() ,
,
在△BOP与△BQC中,
![]() ,
,
∴△BOP![]() △BQC,
△BQC,
∴![]() ,
,
即![]() ,
,
∴BQ=2,
∴OQ=BO-BQ=3,
∴OD=![]() =
=![]() =1,
=1,
综上所述,这个菱形不在圆上的顶点与圆心的距离是1.
故答案是:1.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,点
,点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线与
的垂线与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的函数关系表达式;
(2)当点![]() 在线段
在线段![]() (点
(点![]() 不与
不与![]() 重合)上运动至何处时,线段
重合)上运动至何处时,线段![]() 的长有最大值?并求出这个最大值;
的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点![]() ,连接
,连接![]() .请问:
.请问:![]() 的面积是否存在最大值?若存在,求出此时点
的面积是否存在最大值?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
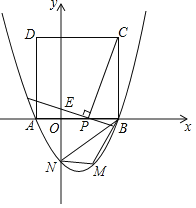
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了清洗水箱,需先放掉水箱内原有的存水,如图是水箱剩余水量y(升)随放水时间x(分)变化的图象.
(1)求y关于x的函数表达式,并确定自变量x的取值范围;
(2)若8:00打开放水龙头,估计8:55﹣9:10(包括8:55和9:10)水箱内的剩水量(即y的取值范围);
(3)当水箱中存水少于10升时,放水时间至少超过多少分钟?
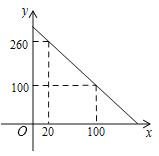
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的一条弦,点
的一条弦,点![]() 在
在![]() 上,联结
上,联结![]() 并延长,交弦
并延长,交弦![]() 于点
于点![]() ,且
,且![]() .
.
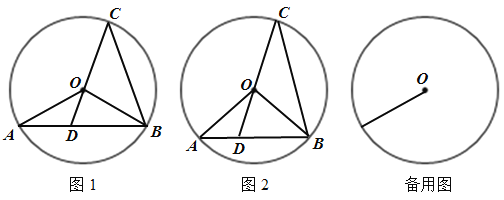
(1)如图1,如果![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,如果![]() ,求
,求![]() 的值;
的值;
(3)延长线段![]() 交弦
交弦![]() 于点
于点![]() ,如果
,如果![]() 是等腰三角形,且
是等腰三角形,且![]() 的半径长等于
的半径长等于![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数y=ax2+2ax﹣3a(a>0)图象的顶点为C,与x轴交于A,B两点(点A在点B的左侧),点C,B关于过点A的直线l对称,直线l与y轴交于D.
(1)求A,B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)在第三象限抛物线上有一个动点E,连接OE交直线l于点F,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
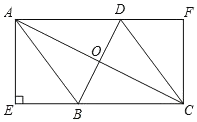
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=8,AD=10,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学号召全校学生进行安全教育网络学习,并对部分学生的学习情况进行了随机调查.对部分学生的成绩(x为整数,满分100分)进行统计,并绘制了如下统计图表.
调查结果频数分布表
| 调查结果扇形统计图
|
根据所给信息,解答下列问题:
(1)填空:![]() _________,
_________,![]() _________;
_________;
(2)求扇形统计图中,m的值及A组对应的圆心角的度数;
(3)若参加学习的同学共有1500人,请你估计成绩不低于80分的同学有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com