
【题目】已知,二次函数y=ax2+2ax﹣3a(a>0)图象的顶点为C,与x轴交于A,B两点(点A在点B的左侧),点C,B关于过点A的直线l对称,直线l与y轴交于D.
(1)求A,B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)在第三象限抛物线上有一个动点E,连接OE交直线l于点F,求![]() 的最大值.
的最大值.
【答案】(1)点A、B的坐标分别为:(﹣3,0)、(1,0),直线l的表达式为:y=﹣![]() x﹣
x﹣![]() ;(2)y=
;(2)y=![]() ;(3)
;(3)![]() .
.
【解析】
(1)对于y=ax2+2ax3a,令y=0,则x=3或1,求出点A、B的坐标,利用点C,B关于直线l对称得AC=AB=4,求出a的值,进而求解;
(2)由(1)得到a的值,故可求解;
(3)利用△HEF∽△DOF,得到![]() =
= =﹣
=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,即可求解.
,即可求解.
(1)对于y=ax2+2ax﹣3a,令y=0,则x=﹣3或1,
则点A、B的坐标分别为:(﹣3,0)、(1,0),
则函数的对称轴为:x=﹣1,则顶点C坐标为:(﹣1,﹣4a),
∵点C,B关于直线l对称,如下图:

∴AC=AB=4,
即(﹣3+1)2+(0+4a)2=42,
解得:a=![]() (负值已舍去),
(负值已舍去),
故点C的坐标为:(﹣1,﹣2![]() ),
),
则BC=![]() =4=AB=AC,
=4=AB=AC,
故△ABC为等边三角形,
∵点C,B关于直线l对称,
则BC∠⊥AD,故∠BAD=30°,
∵tan30°=![]()
则设直线l的表达式为:y=﹣![]() x+b,
x+b,
将点A的坐标代入得0=﹣![]() ×3+b
×3+b
并解得:b=﹣![]() ,
,
故直线l的表达式为:y=﹣![]() x﹣
x﹣![]() ;
;
(2)由(1)知a=![]() ,
,
故抛物线的表达式为:y=![]() x2+
x2+![]() x﹣
x﹣![]() ;
;
(3)∵直线l的表达式为:y=﹣![]() x﹣
x﹣![]() ;
;
∴点D的坐标为:(0,﹣![]() ),即OD=
),即OD=![]() ,
,
过点E作y轴的平行线交AD于点H,
设点E(x,![]() x2+
x2+![]() x﹣
x﹣![]() ),则点H(x,﹣
),则点H(x,﹣![]() x﹣
x﹣![]() ),
),
则EH=(﹣![]() x﹣
x﹣![]() )﹣(
)﹣(![]() x2+
x2+![]() x﹣
x﹣![]() )=﹣
)=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
∵HE∥y轴,
∴△HEF∽△DOF,
∴![]() =
= =﹣
=﹣![]() x2﹣
x2﹣![]() x+
x+![]() =-
=-![]() (x+
(x+![]() )2+
)2+![]() ,
,
∵![]() 0,故
0,故![]() 有最大值,
有最大值,
当x=﹣![]() 时,
时,![]() 最大值为
最大值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
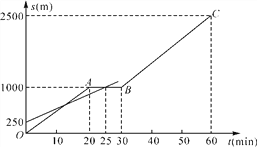
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500 m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目:初中数学 来源: 题型:
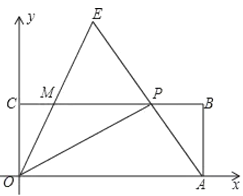
【题目】如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当x为何值时,OP⊥AP?
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“联络四边形”,已知圆的半径长为![]() ,这个圆的一个联络四边形是边长为
,这个圆的一个联络四边形是边长为![]() 的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.
的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
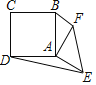
【题目】如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且![]() ,过点C的直线CD
,过点C的直线CD![]() BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
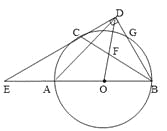
(1)求证:CD是⊙O的切线.
(2)若![]() ,求
,求![]() E的度数.
E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,圆弧盖板侧面
,圆弧盖板侧面![]() 所在圆的圆心
所在圆的圆心![]() 是矩形
是矩形![]() 的中心,绕点
的中心,绕点![]() 旋转开关(所有结果保留小数点后一位).
旋转开关(所有结果保留小数点后一位).
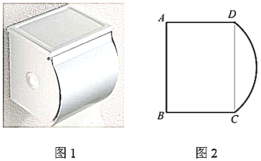
(1)求![]() 所在
所在![]() 的半径长及
的半径长及![]() 所对的圆心角度数;
所对的圆心角度数;
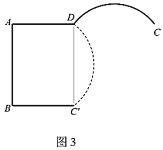
(2)如图3,当圆弧盖板侧面![]() 从起始位置
从起始位置![]() 绕点
绕点![]() 旋转
旋转![]() 时,求
时,求![]() 在这个旋转过程中扫过的的面积.
在这个旋转过程中扫过的的面积.
参考数据:![]() ,
,![]() ,
,![]() 取3.14.
取3.14.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(2m+1)x2+4mx+2m﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数之和等于﹣1?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com