
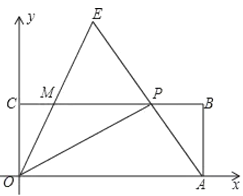
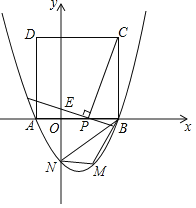
����Ŀ����ͼ����ֱ������ϵxOy�У�����OABC�Ķ���A��C�ֱ���x���y���������ϣ���B�������ǣ�5��2������P��CB����һ���㣨�����C����B�غϣ�������OP��AP������O������OE��AP���ӳ����ڵ�E����CB���ڵ�M���ҡ�AOP=��COM����CP=x��MP=y��
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����xΪ��ֵʱ��OP��AP��
��3���ڵ�P���˶������У��Ƿ����x��ʹ��OCM��������ABP�����֮�͵��ڡ�EMP������������ڣ�����x��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() (
(![]() )����2����
)����2����![]() ʱ��
ʱ��![]() ����3�����ڣ�
����3�����ڣ�![]()
��������
��1��֤��![]() ���õ�
���õ�![]() ���õ�x��y�ĺ�����ϵʽ��
���õ�x��y�ĺ�����ϵʽ��
��2����OP��AP�����֤��![]() ���õ�����x�ķ��̣��ⷽ�̣��Ѳ�������ֵ��ȥ���ɣ�
���õ�����x�ķ��̣��ⷽ�̣��Ѳ�������ֵ��ȥ���ɣ�
��3����E��![]() �ڵ�D����MP�ڵ�F��֤��
�ڵ�D����MP�ڵ�F��֤��![]() ���õ�����y�ķ��̣����y���ڸ��ݣ�1�����x���Ѳ�������ֵ��ȥ���ɣ�
���õ�����y�ķ��̣����y���ڸ��ݣ�1�����x���Ѳ�������ֵ��ȥ���ɣ�
��1����ͼ����BC��OA��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��![]() ��
��
��2����ͼ��������֪��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��![]() ���������⣬��ȥ����
���������⣬��ȥ����
�൱![]() ʱ��
ʱ��![]() ��
��
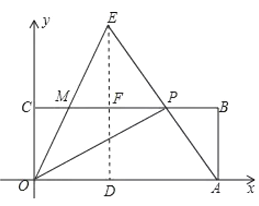
��3���������x�������⣮
��ͼ����E��![]() �ڵ�D����MP�ڵ�F����
�ڵ�D����MP�ڵ�F����![]() ��
��
��![]() ��
��![]() ���֮�͵���
���֮�͵���![]() �������
�������
��![]() ��
��
��![]() ��
��![]() ��
��
��PM��OA��
��![]() ��
��
��![]() ��
��
��![]() �����
�����![]() ��
��
���ɣ�2��![]() �ã�
�ã�![]() ��
��
���![]() ��
��![]() ��������������ȥ����
��������������ȥ����
���ڵ�P���˶������У�����![]() ��ʹ
��ʹ![]() ��
��![]() ���֮�͵���
���֮�͵���![]() �������
�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�H�ǶԽ���BD���е㣬�ӳ�DC��E��ʹ��DE=DB������BE����DF��BE��BC�ڵ�G����BE�ڵ�F������CH��FH�����н��ۣ���1��HC=HF����2��DG=2EF����3��BE��DF=2CD2����4��S��BDE=4S��DFH����5��HF��DE����ȷ�ĸ����ǣ� ��

A.5B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm����BAC=60��������M�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����N�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
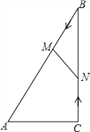
��1����BM=BN����t��ֵ��
��2������MBN���ABC���ƣ���t��ֵ��
��3����tΪ��ֵʱ���ı���ACNM�������С���������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�������ɽ���棬�����³�������ɽ�³��ĵ��侭����A�����Bʱ����������200 m���³���ʻ��·����ˮƽ�н��Ϧ�=16�������³������ɵ�B�����Dʱ�������߹���200 m���³��ɵ�B����D����ʻ·����ˮƽ�н��Ϧ�=42�������³��ӵ�A����D��ֱ�����ľ��룮������������������ο����ݣ�sin16���0.27��cos16���0.77��sin42���0.66��cos42���0.74��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ţ�5����Ϊ���˽�ȫ��ѧ��ϲ���������������ȡȫ�����ķ�����������ƹ��������������ĸ����������ȫ��ѧ������Ȥ���ã����ݵ���Ľ���齨��4����ȤС�飬�����Ƴ����µ�������������ͳ��ͼ����ͼ�٣��ڣ�Ҫ��ÿλѧ��ֻ��ѡ��һ���Լ�ϲ�������ࣩ���������ͼ���ṩ����Ϣ����������⣺
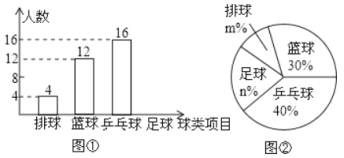
��1���ţ�5�����ѧ������Ϊ_________����������ͳ��ͼ����������
��2������ͳ��ͼ��n=__________��m=___________��
��3��������ȤС��4��ѧ������2��2Ů�����ڴ���������ѡ��2��ѧ���μ�ѧУ������ӣ������б�����״ͼ�ķ�����ѡ����2��ѧ��ǡ����һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() �͵�
�͵�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����
Ϊ����![]() ���Ϸ���������
���Ϸ���������![]() ����
����![]() ��
��![]() ����һ���㣬����
����һ���㣬����![]() ������
������![]() ��
��![]() �Ĵ�����
�Ĵ�����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1����������ߵĺ�����ϵ����ʽ��
��2������![]() ���߶�
���߶�![]() ����
����![]() ����
����![]() �غϣ����˶����δ�ʱ���߶�
�غϣ����˶����δ�ʱ���߶�![]() �ij������ֵ�������������ֵ��
�ij������ֵ�������������ֵ��
��3���ڵ�����������������ȡһ��![]() ������
������![]() �����ʣ�
�����ʣ�![]() ������Ƿ�������ֵ�������ڣ������ʱ��
������Ƿ�������ֵ�������ڣ������ʱ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
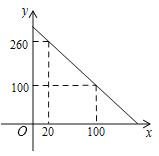
����Ŀ��Ϊ����ϴˮ�䣬���ȷŵ�ˮ����ԭ�еĴ�ˮ����ͼ��ˮ��ʣ��ˮ��y���������ˮʱ��x���֣��仯��ͼ��
��1����y����x�ĺ�������ʽ����ȷ���Ա���x��ȡֵ��Χ��
��2����8��00��ˮ��ͷ������8��55��9��10������8��55��9��10��ˮ���ڵ�ʣˮ������y��ȡֵ��Χ����
��3����ˮ���д�ˮ����10��ʱ����ˮʱ�����ٳ������ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
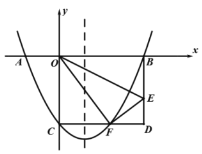
����Ŀ����֪�����κ���y��ax2+2ax��3a��a��0��ͼ��Ķ���ΪC����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����C��B���ڹ���A��ֱ��l�Գƣ�ֱ��l��y�ύ��D��
��1����A��B�������꼰ֱ��l�Ľ���ʽ��
��2������κ�������ʽ��
��3���ڵ�����������������һ������E������OE��ֱ��l�ڵ�F����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��۵�����![]() ��һ��
��һ��![]() ��ʹ��
��ʹ��![]() ����
����![]() �ߵĵ�
�ߵĵ�![]() �����ۺ�Ϊ
�����ۺ�Ϊ![]() ������
������![]() ����֪��
����֪��![]() ������Ϊ
������Ϊ![]() �����κ���
�����κ���![]() ͼ��
ͼ��![]() ��
��![]() ��
��![]() ���㣮
���㣮
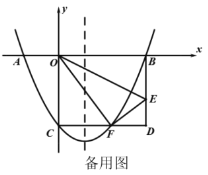
��1����������ʽ��
��2����![]() ���·�����������һ����
���·�����������һ����![]() ������
������![]() ��
��![]() �ᣬ��
�ᣬ��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����
����![]() ��
��![]() ����ʱ�����
����ʱ�����![]() �����꣮
�����꣮
��3���������߶Գ������Ƿ����һ��![]() ��ʹ
��ʹ![]() �����ֵ�������ڣ���ֱ��д��
�����ֵ�������ڣ���ֱ��д��![]() ������ꣻ�������ڣ���˵�����ɣ�
������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com