
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且![]() ,过点C的直线CD
,过点C的直线CD![]() BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
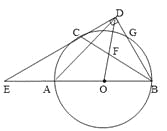
(1)求证:CD是⊙O的切线.
(2)若![]() ,求
,求![]() E的度数.
E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
【答案】(1)证明见解析;(2)∠E=30°;(3)AD=![]() .
.
【解析】
试题(1)如图1,连接OC,AC,CG,由圆周角定理得到∠ABC=∠CBG,根据同圆的半径相等得到OC=OB,于是得到∠OCB=∠OBC,等量代换得到∠OCB=∠CBG,根据平行线的判定得到OC∥BG,即可得到结论;(2)由OC∥BD,得到△OCF∽△BDF,△EOC∽△EBD,得到![]() ,
,![]() ,根据直角三角形的性质即可得到结论;(3)如图2,过A作AH⊥DE于H,解直角三角形得到BD=3,DE=3
,根据直角三角形的性质即可得到结论;(3)如图2,过A作AH⊥DE于H,解直角三角形得到BD=3,DE=3![]() ,BE=6,在Rt△DAH中,AD=
,BE=6,在Rt△DAH中,AD=![]() =
=![]() =
=![]() .
.
试题解析:(1)证明:如图1,连接OC,AC,CG,
∵AC=CG,∴![]() ,∴∠ABC=∠CBG,
,∴∠ABC=∠CBG,
∵OC=OB,∴∠OCB=∠OBC,∴∠OCB=∠CBG,∴OC∥BG,
∵CD⊥BG,∴OC⊥CD,∴CD是⊙O的切线;
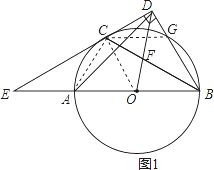
(2)解:∵OC∥BD,∴△OCF∽△BDF,△EOC∽△EBD,
∴![]() ,∴
,∴![]() ,
,
∵OA=OB,∴AE=OA=OB,∴OC=![]() OE,
OE,
∵∠ECO=90°,∴∠E=30°;
(3)解:如图2,过A作AH⊥DE于H,
∵∠E=30°∴∠EBD=60°,∴∠CBD=![]() EBD=30°,
EBD=30°,
∵CD=![]() ,∴BD=3,DE=3
,∴BD=3,DE=3![]() ,BE=6,∴AE=
,BE=6,∴AE=![]() BE=2,
BE=2,
∴AH=1,∴EH=![]() ,∴DH=2
,∴DH=2![]() ,
,
在Rt△DAH中,AD=![]() =
=![]() =
=![]() .
.
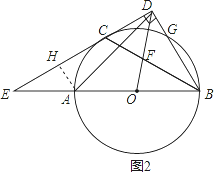
故答案为(1)证明见解析;(2)∠E=30°;(3)AD=![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
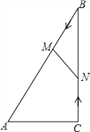
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
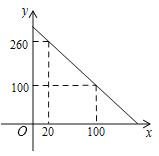
【题目】为了清洗水箱,需先放掉水箱内原有的存水,如图是水箱剩余水量y(升)随放水时间x(分)变化的图象.
(1)求y关于x的函数表达式,并确定自变量x的取值范围;
(2)若8:00打开放水龙头,估计8:55﹣9:10(包括8:55和9:10)水箱内的剩水量(即y的取值范围);
(3)当水箱中存水少于10升时,放水时间至少超过多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数y=ax2+2ax﹣3a(a>0)图象的顶点为C,与x轴交于A,B两点(点A在点B的左侧),点C,B关于过点A的直线l对称,直线l与y轴交于D.
(1)求A,B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)在第三象限抛物线上有一个动点E,连接OE交直线l于点F,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
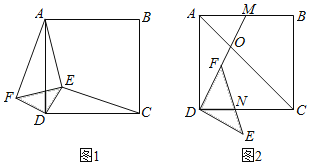
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE=1:![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的边DF与边DM重合时(如图2),若OF=![]() ,求DF和DN的长.
,求DF和DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
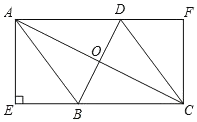
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=8,AD=10,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AD与圆相切,请在下图中,仅用无刻度的直尺按要求画图.
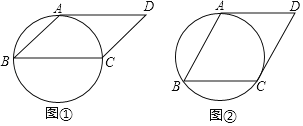
(1)若BC是圆的直径,画出平行四边形ABCD的边CD上的高;
(2)若CD与圆相切,画出平行四边形ABCD的边BC上的高AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,折叠矩形![]() 的一边
的一边![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处,折痕为
处,折痕为![]() ,连接
,连接![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 图象经过
图象经过![]() 、
、![]() 、
、![]() 三点.
三点.
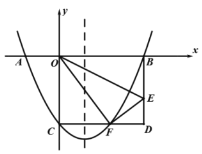
(1)求函数解析式;
(2)在![]() 轴下方抛物线上有一动点
轴下方抛物线上有一动点![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,当
,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
(3)在抛物线对称轴上是否存在一点![]() ,使
,使![]() 有最大值?若存在,请直接写出
有最大值?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:
问题:如图1,等边三角形ABC的边长为6,点O是∠ABC和∠ACB的角平分线交点,∠FOG=120°,绕点O任意旋转∠FOG,分别交△ABC的两边于D,E两点求四边形ODBE的面积.
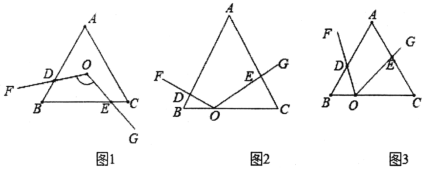
讨论:
①甲:在∠FOG旋转过程中,当OF经过点B时,OG一定经过点C.
②乙:小明的分析有道理,这样,我们就可以利用“ASA”证出△ODB≌△OEC.
③丙:因为△ODB≌△OEC,所以只要算出△OBC的面积就得出了四边形ODBE的面积.
老师:同学们的思路很清晰,也很正确,在分析和解决问题时,我们经常会借用特例作辅助线来解决一般问题请你按照探究的思路,直接写出四边形ODBE的面积:________.
(2)应用:
①特例:如图2,∠FOG的顶点O在等边三角形ABC的边BC上,OB=2,OC=4,边OG⊥AC于点E,OF⊥AB于点D,求△BOD面积.
②探究:如图3,已知∠FOG=60°,顶点O在等边三角形ABC的边BC上,OB=2,OC=4,记△BOD的面积为x,△COE的面积为y,求xy的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com