
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
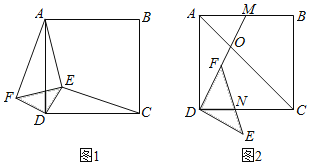
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE=1:![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的边DF与边DM重合时(如图2),若OF=![]() ,求DF和DN的长.
,求DF和DN的长.
【答案】(1)CE=AF,见解析;(2)∠AED=135°;(3)![]() ,
,![]() .
.
【解析】
(1)由正方形和等腰直角三角形的性质判断出△ADF≌△CDE即可;
(2)设DE=k,表示出AE,CE,EF,判断出△AEF为直角三角形,即可求出∠AED;
(3)由AB∥CD,得出![]() ,求出DM,DO,再判断出△DFN∽△DCO,得到
,求出DM,DO,再判断出△DFN∽△DCO,得到![]() ,求出DN、DF即可.
,求出DN、DF即可.
解:(1)CE=AF,
在正方形ABCD和等腰直角三角形CEF中,FD=DE,CD=AD,∠ADC=∠EDF=90°,
∴∠ADF=∠CDE,
∴△ADF≌△CDE(SAS),
∴CE=AF;
(2)设DE=k,
∵DE:AE:CE=1:![]() :3
:3
∴AE=![]() k,CE=AF=3k,
k,CE=AF=3k,
∴EF=![]() k,
k,
∵AE2+EF2=7k2+2k2=9k2,AF2=9k2,
即AE2+EF2=AF2
∴△AEF为直角三角形,
∴∠AEF=90°
∴∠AED=∠AEF+DEF=90°+45°=135°;
(3)∵M是AB的中点,
∴MA=![]() AB=
AB=![]() AD,
AD,
∵AB∥CD,
∴△MAO∽△DCO,
∴![]() ,
,
在Rt△DAM中,AD=4,AM=2,
∴DM=2![]() ,
,
∴DO=![]() ,
,
∵OF=![]() ,
,
∴DF=![]() ,
,
∵∠DFN=∠DCO=45°,∠FDN=∠CDO,
∴△DFN∽△DCO,
∴![]() ,即
,即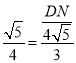 ,
,
∴DN=![]() .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=BE=4,AE=3,求CD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙,无重叠的四边形EFGH,设AB=a,BC=b,若AH=1,则( )
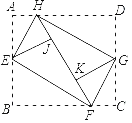
A.a2=4b﹣4B.a2=4b+4C.a=2b﹣1D.a=2b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
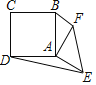
【题目】如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
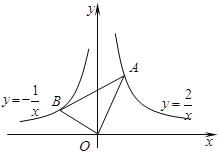
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且![]() ,过点C的直线CD
,过点C的直线CD![]() BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
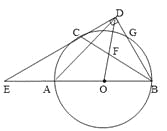
(1)求证:CD是⊙O的切线.
(2)若![]() ,求
,求![]() E的度数.
E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,-2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.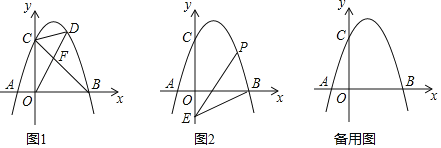
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
(1)依据题意补充完整图形;(尺规作图,保留作图痕迹,不写作法)
(2)求证:![]() 与直线
与直线![]() 相切;
相切;
(3)在(2)的条件下,若![]() 与直线
与直线![]() 相切的切点为
相切的切点为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ;其中
;其中![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________.
倍,得到矩形A2OC2B2,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________.
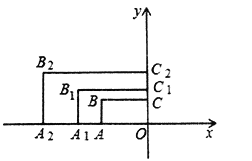
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com