
分析 (1)根据函数的解析式作出函数的图象,然后描述其所处的位置及其增减性即可;
(2)根据函数图象平移规律:左加右减上加下减,可得答案.
解答 解:(1)函数y=$\frac{2}{{x}^{2}}$的图象如下图: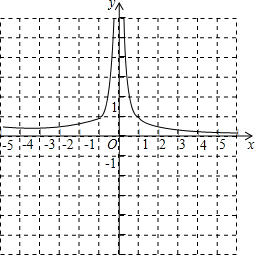
函数的图象是双曲线,两个分支分别位于一、二象限,在第二象限y随着x的增大而增大,在第一象限y随着x的增大而减小;
(2)如图:
y=$\frac{2}{{x}^{2}}$的图象向下平移两个单位得①y=$\frac{2}{{x}^{2}}$-2
y=$\frac{2}{{x}^{2}}$的图象向右平移一个单位得y=$\frac{2}{(x-1)^{2}}$.
点评 本题考查了反比例函数的图象及性质,解题的关键是正确的作出反比例函数的图象,难度不大.


科目:初中数学 来源: 题型:选择题
 如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )| A. | 3个 | B. | 5个 | C. | 7个 | D. | 8个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
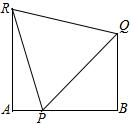 设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.
设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,A是直线上的一个点,请你在A点的右侧每隔1厘米取一个点,共取三个点,那么
如图所示,A是直线上的一个点,请你在A点的右侧每隔1厘米取一个点,共取三个点,那么查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com