
�������ܣ����ɶ����Ǽ���ѧ�е����飬������������ǧ�����������Ƕ�����֤����֮������������������ѧ�ң�Ҳ��ҵ����ѧ�����ߣ�����1994�깹�췢����һ���µ�֤����
С��ţ����������ȫ�ȵ�ֱ����������ͼ1���ã������߳��ֱ�Ϊa��b��c����Ȼ��
��DAB=��B=90�㣬AC��DE������a��b��c�ֱ��ʾ������ABCD���ı���AECD����EBC���������̽��������ͼ�����֮��Ĺ�ϵ���ɵõ����ɶ�����

S����ABCD= ��
S��ABC= ��
S�ı���AECD= ��
����������Ĺ�ϵʽΪ �����ɵõ����ɶ�����
֪ʶ���ã�
��1����ͼ2����·��A��B���㣨����ֱ���ϵ����㣩���40ǧ�ף�C��DΪ������ׯ�����������㣩��AD��AB��BC��AB������ֱ�ΪA��B��AD=25ǧ�ף�BC=16ǧ�ף���������ׯ�ľ���Ϊ ǧ�ף�ֱ����գ���
��2���ڣ�1���ı����£���AB=40ǧ�ף�AD=24ǧ�ף�BC=16ǧ�ף�Ҫ��AB�Ͻ���һ����ӦվP��ʹ��PC=PD�����ó߹���ͼ��ͼ2������P���λ�ò����AP�ľ��룮
֪ʶǨ�ƣ����������˼�������뼸��ģ�ͣ������ʽ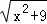
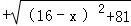 ����Сֵ��0��x��16��
����Сֵ��0��x��16��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ��ɽ��ʡ�������Ľ��ذ��꼶��ѧ����ĩ��ѧ�Ծ��������棩 ���ͣ������
��2015��•��������ĩ����m= ʱ������x�ķ���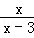 =2��
=2��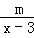 �⣮
�⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���꼶�ϵ�һ���¿���ѧ���������棩 ���ͣ������
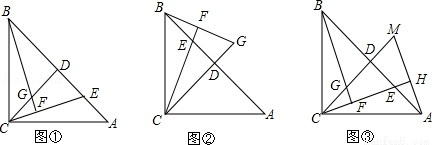
��2015��•�ˮ����ĩ����֪���ڡ�ABC�У�AC=BC����ACB=90�㣬����C��CD��AB�ڵ�D����E��AB����һ���㣨�����˵�A��B��������CE������B��CE�Ĵ��߽�ֱ��CE�ڵ�F����ֱ��CD�ڵ�G����ͼ�٣���
��1����֤��AE=CG��
��2������E�˶����߶�BD��ʱ����ͼ�ڣ����Բ���AE��CG��������ϵ�Ƿ����仯����ֱ��д����Ľ��ۣ�
��3������A��AH��ֱ��ֱ��CE������Ϊ��H������CD���ӳ����ڵ�M����ͼ�ۣ����ҳ�ͼ����BE��ȵ��߶Σ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���꼶�ϵ�һ���¿���ѧ���������棩 ���ͣ������
��2015��•������ĩ����ͼ����1=��2��Ҫʹ��ABD�ա�ACD�������ӵ�һ�������� ��ֻ��һ���������ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���꼶�ϵ�һ���¿���ѧ���������棩 ���ͣ�ѡ����
��2010•���ϣ���ͼ��a��b��c�ֱ��ʾ��ABC�����߳������������ABCһ��ȫ�ȵ��������ǣ� ��
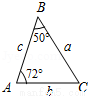
A��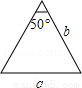 B��
B��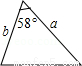 C��
C��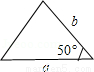 D��
D��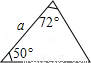
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���꼶�ϵ�14��������ѧ���������棩 ���ͣ�������
��2015��•���������У������⣮
��1��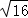 ��
��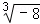 +20150��
+20150��
��2��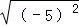 +|1��
+|1��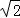 |����
|����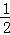 ����2��
����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ���꼶�ϵ�14��������ѧ���������棩 ���ͣ������
��2015��•��ɽУ�����У���֪��P��x��y���ڵ������ޣ���|x|=3��|y|=5�����P�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ̩���а��꼶��ѧ��������ѧ�Ծ��������棩 ���ͣ������
��2014��•���������У����յ��㵺���˳������Һ��ബ�Ӵ���㵺�����Ѳ��άȨ���ȣ���ͼ��OA��OB��OA=45���OB=15������㵺λ��O�㣬�ҹ����ബ�ڵ�B��������һ�����������洬����A���������AO��������ʻ����㵺���ڵص�O���ҹ����ബ������B����������ͬ���ٶ���ijֱ��ȥ���������洬������ڵ�C����ס���洬��

��1������ֱ�ߺ�Բ������C����λ�ã�
��2�����ҹ����ബ��ʻ�ĺ���BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ��ͨ�к����а��꼶��ѧ����ĩ��ѧ�Ծ��������棩 ���ͣ������
��2013•���ݣ��ֽ���ʽ��x2y��4y= ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com