
【题目】市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=45时,y=10;x=55时,y=90.在销售过程中,每天还要支付其他费用500元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围;
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
【答案】(1)y=﹣2x+200(30≤x≤60);(2)W=﹣2x2+260x﹣6500;(3)当销售单价为60元时,该公司日获利最大为1900元.
【解析】
(1)根据y与x成一次函数解析式,设为y=kx+b,把x与y的两对值代入求出k与b的值,即可确定出y与x的解析式,并求出x的范围即可;
(2)根据利润=单个利润×销售量-500列出W关于x的二次函数解析式即可;
(3)利用二次函数的性质求出W的最大值,以及此时x的值即可.
(1)设y=kx+b,
∵x=45时,y=10;x=55时,y=90,
∴![]() ,
,
解得:k=﹣2,b=200,
∴y=﹣2x+200(30≤x≤60);
(2)∵售价为x元/千克,进价为30元/千克,日销量y=﹣2x+200,每天支付其他费用500元,
∴W=(x﹣30)(﹣2x+200)﹣500=﹣2x2+260x﹣6500,
(3)∵W=﹣2x2+260x﹣6500=﹣2(x﹣65)2+1950,
∴抛物线的对称轴为x=65,
∵-2<0,
∴抛物线开口向下,x<65时,y随x的增大而增大,
∵30≤x≤60,
∴x=60时,w有最大值为-2(60-65)2+1950=1900(元),
∴当销售单价为60元时,该公司日获利最大为1900元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某小组作“用频率估计概率的实验”时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
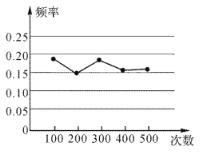
A.掷一个质地均匀的正六面体骰子,向上的面点数是4
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红色
D.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
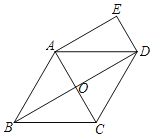
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化已引起社会各界的高度关注,有关部门在全国范围内对12~35岁的网瘾人群进行了随机抽样查,得到了如下两个不定整的统计图,请根据图中信息解答下列问题:
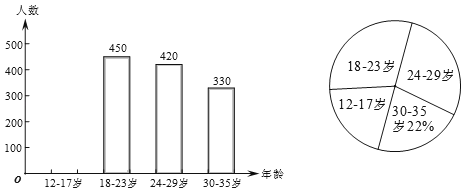
(1)求本次调查了多少名网瘾人员?
(2)通过计算补全条形统计图,在扇形统计图中,18~23岁部分的圆心角的度数为 ;
(3)目前我国12﹣35岁网瘾人数约为3000万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m﹣2)x﹣![]() =0.
=0.
(1)求证:无论m为何值,方程总有两个不相等实数根.
(2)设方程的两实数根为x1,x2,且满足(x1+x2)2=|x1|﹣|x2|+2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
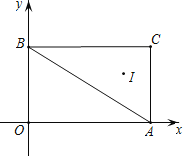
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com