
【题目】如图所示,![]() 是平角,
是平角,![]() 分别是
分别是![]() 的平分线.
的平分线.
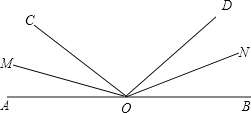
(1)已知![]() ,求
,求![]() 的度数;
的度数;
(2)如果(1)中的已知“![]() ”,改为已知“
”,改为已知“![]() ”,你能求出
”,你能求出![]() 的度数吗?如果能,请求出;如果不能,请说明理由.
的度数吗?如果能,请求出;如果不能,请说明理由.
【答案】(1)135°(2)能.135°.
【解析】
(1)根据平角即可求得∠AOB的度数,再根据角平分线的定义求得∠AOM和∠BON的度数,从而求得∠MON的度数;
(2)因为OM、ON分别是∠AOC、∠BOD的平分线,故知∠MOC+∠NOD=![]() ∠AOC+
∠AOC+![]() ∠BOD=
∠BOD=![]() (∠AOC+∠BOD)即可解答.
(∠AOC+∠BOD)即可解答.
(1)∵∠AOB是平角,∠AOC=42°,∠BOD=48°,
∴∠COD=∠AOB∠AOC∠BOD=180°42°48°=90°,
∵OM、ON分别是∠AOC、∠BOD的平分线,
∴∠MOC=![]() ∠AOC=21°,∠NOD=
∠AOC=21°,∠NOD=![]() ∠BOD=24°,
∠BOD=24°,
∴∠MON=∠MOC+∠COD+∠NOD=21°+90°+24°=135°;
(2)能.
∵OM、ON分别是∠AOC、∠BOD的平分线.
∴∠MOC+∠NOD,
=![]() ∠AOC+
∠AOC+![]() ∠BOD,
∠BOD,
=![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
=![]() (180°90°)=45°,
(180°90°)=45°,
∴∠MON=∠MOC+∠NOD+∠COD=90°+45°=135°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4.
(1)建立适当的平面直角坐标系,写出各个顶点的坐标;
(2)将△ABC向左平移5个单位,请在图中画出平移后的△A1B1C1;
(3)将△A1B1C1绕点C1按逆时针旋转90°,请在图中画出旋转后的△A2B2C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
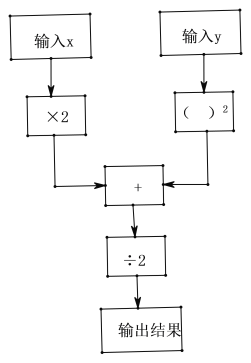
【题目】如图是一个数值转换机的示意图.
(1)请观察示意图,理解运算原理,用代数式表示出来输出的结果 ;
(2)若小倩输入![]() 的值为3,
的值为3,![]() 的值为-2,小旺输入
的值为-2,小旺输入![]() 的值为-3,
的值为-3,![]() 的值为2,若设定输出的结果数大的获胜,他俩谁胜出啦?
的值为2,若设定输出的结果数大的获胜,他俩谁胜出啦?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,,
,,![]()
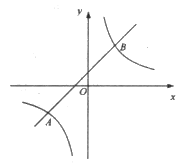
(1)求反比例函数与一次函数的函数表达式
(2)请结合图像直接写出不等式![]() 的解集;
的解集;
(3)若点P为x轴上一点,△ABP的面积为10,求点P的坐标,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下)
(1)写出D级学生的人数占全班总人数的百分比为 ,C级学生所在的扇形圆心角的度数为 ;
(2)该班学生体育测试成绩的中位数落在等级 内;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
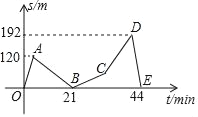
【题目】爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题:
(1)小芳和爸爸上山时的速度各是多少?
(2)求出爸爸下山时CD段的函数解析式;
(3)因山势特点所致,二人相距超过120m就互相看不见,求二人互相看不见的时间有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
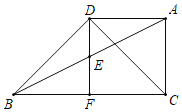
【题目】如图:在△ABC中,点E,F分别是BA,BC边的中点,过点A作AD∥BC交FE的延长线于点D,连接DB,DC.
(1)求证:四边形ADFC是平行四边形;
(2)若∠BDC=90°,求证:CD平分∠ACB;
(3)在(2)的条件下,若BD=DC=6,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com