
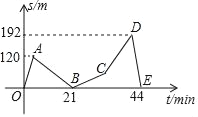
【题目】爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题:
(1)小芳和爸爸上山时的速度各是多少?
(2)求出爸爸下山时CD段的函数解析式;
(3)因山势特点所致,二人相距超过120m就互相看不见,求二人互相看不见的时间有多少分钟?
【答案】(1)小芳上山的速度为20m/min,爸爸上山的速度为28m/min;(2)爸爸下山时CD段的函数解析式为y=12x﹣288(24≤x≤40);(3)二人互相看不见的时间有7.5分钟.
【解析】分析:(1)根据速度=路程÷时间可求出小芳上山的速度;根据速度=路程÷时间+小芳的速度可求出爸爸上山的速度;
(2)根据爸爸及小芳的速度结合点C的横坐标(6+24=30),可得出点C的坐标,由点D的横坐标比点E少4可得出点D的坐标,再根据点C、D的坐标利用待定系数法可求出CD段的函数解析式;
(3)根据点D、E的坐标利用待定系数法可求出DE段的函数解析式,分别求出CD、DE段纵坐标大于120时x的取值范围,结合两个时间段即可求出结论.
详解:(1)小芳上山的速度为120÷6=20(m/min),
爸爸上山的速度为120÷(21﹣6)+20=28(m/min).
答:小芳上山的速度为20m/min,爸爸上山的速度为28m/min.
(2)∵(28﹣20)×(24+6﹣21)=72(m),
∴点C的坐标为(30,72);
∵二人返回山下的时间相差4min,44﹣4=40(min),
∴点D的坐标为(40,192).
设爸爸下山时CD段的函数解析式为y=kx+b,
将C(30,72)、D(40,192)代入y=kx+b,
![]() ,解得:
,解得:![]() .
.
答:爸爸下山时CD段的函数解析式为y=12x﹣288(24≤x≤40).
(3)设DE段的函数解析式为y=mx+n,
将D(40,192)、E(44,0)代入y=mx+n,
![]() ,解得:
,解得:![]() ,
,
∴DE段的函数解析式为y=﹣48x+2112(40≤x≤44).
当y=12x﹣288>120时,34<x≤40;
当y=﹣48x+2112>120时,40≤x<41.5.
41.5﹣34=7.5(min).
答:二人互相看不见的时间有7.5分钟.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以“绿色生活,美丽家园”为主题的2019年中国北京世界园艺博览会(简称北京世园会)已拉开帷幕,讲述人与自然和谱共生的精彩故事,世园会甲工程队制作园艺造型300个与乙工程队制作园艺造型400个所用时间相等,乙工程队每天比甲工程队多制作10个园艺造型,求甲工程队每天制作园艺造型多少个?
两名同学所列的方程如下:
![]()
根据以上信息,解答下列问题:
(1)小明同学所列方程中的x表示 ,小红同学所列方程中的y表 ;
(2)根据你选择的方程,求出甲工程队每天制作园艺造型多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
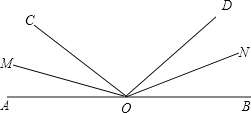
【题目】如图所示,![]() 是平角,
是平角,![]() 分别是
分别是![]() 的平分线.
的平分线.
(1)已知![]() ,求
,求![]() 的度数;
的度数;
(2)如果(1)中的已知“![]() ”,改为已知“
”,改为已知“![]() ”,你能求出
”,你能求出![]() 的度数吗?如果能,请求出;如果不能,请说明理由.
的度数吗?如果能,请求出;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和利润如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元/瓶) | 50 | 35 |
利润(元/瓶) | 20 | 15 |
(1)请求出y关于x的函数关系式;
(2)如果该厂每天至少投入成本26 400元,那么每天至少获利多少元?
(3)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
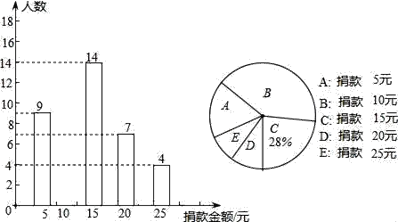
(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 平均数是 中位数为
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
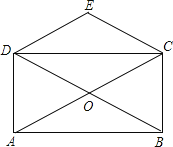
【题目】如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
(1)证明:四边形OCED为菱形;
(2)若AC=4,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划修建一条长60千米的地铁,根据甲,乙两个地铁修建公司标书数据发现:甲,乙两公司每天修建地铁长度之比为3:5;甲公司单独完成此项工程比乙公司单独完成此项工程要多用240天.
(1)求甲,乙两个公司每天分别修建地铁多少千米?
(2)该市规定:“该工程由甲,乙两个公司轮流施工完成,工期不超过450天,且甲公司工作天数不少于乙公司工作天数的![]() ”.设甲公司工作a天,乙公司工作b天.
”.设甲公司工作a天,乙公司工作b天.
①请求出b与a的函数关系式及a的取值范围;
②设完成此项工程的工期为W天,请求出W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
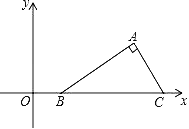
【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
A. (﹣4,﹣2﹣![]() ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+![]() ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+![]() ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com