
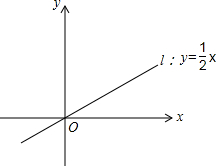 如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.
如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.分析 (1)根据直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$,可以得到点A的坐标;
(2)根据题意可知符合条件的点B有四个,画出相应的图形,求出四种情况下点B的坐标,从而可以解答本题.
解答 解:(1)设点A的坐标为(x,0.5x)(x>0),
∵OA=$\sqrt{5}$,
∴$\sqrt{{x}^{2}+(0.5x)^{2}}=\frac{\sqrt{5}x}{2}=\sqrt{5}$,
解得x=2,
∴点A的坐标为(2,1).
即点A的坐标为(2,1).
(2)根据题意满足条件的点B有三个,如下图所示: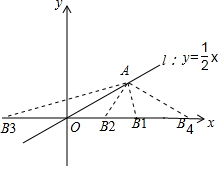
当OA=OB1时,由OA=$\sqrt{5}$可得点B1的坐标为($\sqrt{5},0$);
当OB2=AB2时,设B2的坐标为(a,0),则$\sqrt{(2-a)^{2}+{1}^{2}}=a$,
解得,a=$\frac{5}{4}$,
故点B2的坐标为($\frac{5}{4},0$);
当OA=OB3时,由OA=$\sqrt{5}$可得点B3的坐标为($-\sqrt{5},0$);
当AO=AB4时,点B4的坐标为(4,0);
由上可得,满足条件的点B的坐标为:($\sqrt{5},0$)或($\frac{5}{4},0$)或($-\sqrt{5},0$)或(4,0).
点评 本题考查一次函数图象上点的坐标的特征,解题的关键是利用数形结合的思想,灵活变化,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
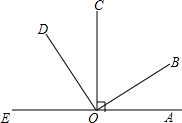 看图回答下列问题:
看图回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com