
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复上述过程,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.64 | 0.58 | 0.605 | 0.601 |
(1)请将表中的数据补充完整,
(2)请估计:当n很大时,摸到白球的概率约是 .(精确到0.1)
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
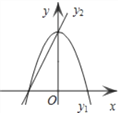
下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是![]() 或
或![]() .其中正确的个数是( )
.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点![]() .点
.点![]() 是原点,固定不动,点
是原点,固定不动,点![]() 和
和![]() 可以移动,点
可以移动,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() .
.
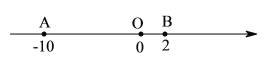
(1)点![]() 与点
与点![]() 之间的距离
之间的距离![]() _______.
_______.
(2)若![]() 点不动,点
点不动,点![]() 向右每秒移动
向右每秒移动![]() 个单位长,移动时间为
个单位长,移动时间为![]() 秒,此时点
秒,此时点![]() 与点
与点![]() 之间的距离
之间的距离![]() ________(用含
________(用含![]() 的代数式表示).
的代数式表示).
(3)若点![]() 向右每秒移动
向右每秒移动![]() 个单位长,点
个单位长,点![]() 同时向左每秒移动
同时向左每秒移动![]() 个单位长,设
个单位长,设![]() 为
为![]() 中点,当
中点,当![]() 相差
相差![]() 个单位长时,求
个单位长时,求![]() 点表示的数.
点表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南江县在“创国家级卫生城市”中,朝阳社区计划对某区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区实施课堂教学改革后,学生的自主学习、合作交流能力有很大提高,为了解学生自主学习、合作交流的具体情况,张老师对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
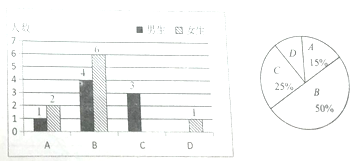
(1)本次调查中,张老师一共调查了_____名同学;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
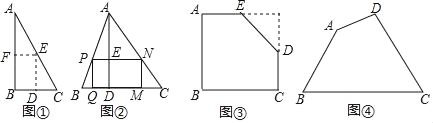
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE,OF,OG分别是∠AOC,∠BOD,∠BOC的平分线,以下说法不正确的是( )
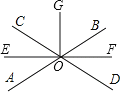
A.∠DOF与∠COG互为余角
B.∠COG与∠AOG互为补角
C.射线OE,OF不一定在同一条直线上
D.射线OE,OG互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
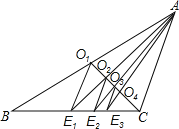
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn= AC.(用含n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com