[题目]如图.正方形ABCD的边长为2cm.动点P从点A出发.在正方形的边上沿A→B→C的方向运动到点C停止.设点P的运动路程为x(cm).在下列图象中.能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )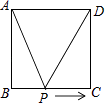A.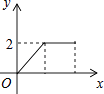B.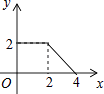C.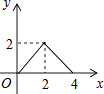D.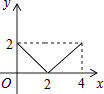 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，正方形ABCD的边长为2cm，动点P从点A出发，在正方形的边上沿A→B→C的方向运动到点C停止，设点P的运动路程为x（cm），在下列图象中，能表示△ADP的面积y（cm2）关于x（cm）的函数关系的图象是（　　）

A.
B.
C.
D.

【答案】A
【解析】解：当P点由A运动到B点时，即0≤x≤2时，y= ×2x=x，
当P点由B运动到C点时，即2＜x＜4时，y= ×2×2=2，
符合题意的函数关系的图象是A；
故选：A．
△ADP的面积可分为两部分讨论，由A运动到B时，面积逐渐增大，由B运动到C时，面积不变，从而得出函数关系的图象．本题考查了动点函数图象问题，用到的知识点是三角形的面积、一次函数，在图象中应注意自变量的取值范围．

练习册系列答案

寒假课程练习南方出版社系列答案

一路领先寒假作业河北美术出版社系列答案

寒假作业美妙假期云南科技出版社系列答案

归类加模拟考试卷新疆文化出版社系列答案

全程达标小升初模拟加真题考试卷新疆美术摄影出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．
（1）请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；
（2）小明选择哪家快递公司更省钱？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】问题探究：
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．
②解决问题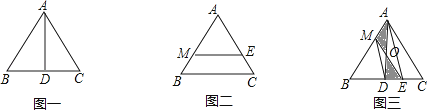

已知等边三角形ABC的边长为2．
（1）如图一，若AD⊥BC，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；
（2）如图二，若ME∥BC，且ME是△ABC的一条面径，求面径ME的长；
（3）如图三，已知D为BC的中点，连接AD，M为AB上的一点（0＜AM＜1），E是DC上的一点，连接ME，ME与AD交于点O，且S△MOA=S△DOE ．
①求证：ME是△ABC的面径；
②连接AE，求证：MD∥AE；
（4）请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】【操作发现】在计算器上输入一个正数，不断地按“ ”键求算术平方根，运算结果越来越接近1或都等于1．
【提出问题】输入一个实数，不断地进行“乘以常数k，再加上常数b”的运算，有什么规律？
【分析问题】我们可用框图表示这种运算过程（如图a）．
也可用图象描述：如图1，在x轴上表示出x1 ，先在直线y=kx+b上确定点（x1 ， y1），再在直线y=x上确定纵坐标为y1的点（x2 ， y1），然后再x轴上确定对应的数x2 ， …，以此类推．
【解决问题】研究输入实数x1时，随着运算次数n的不断增加，运算结果x，怎样变化．

（1）若k=2，b=﹣4，得到什么结论？可以输入特殊的数如3，4，5进行观察研究；
（2）若k＞1，又得到什么结论？请说明理由；
（3）①若k=﹣ ，b=2，已在x轴上表示出x1（如图2所示），请在x轴上表示x2 ， x3 ， x4 ，并写出研究结论；
②若输入实数x1时，运算结果xn互不相等，且越来越接近常数m，直接写出k的取值范围及m的值（用含k，b的代数式表示）