
【题目】如图 1,在第四象限的矩形 ABCD,点 A 与坐标原点 O 重合,且 AB=4,AD=3.点 Q 从 B点出发以每秒 1 个单位长度的速度沿 B→C→D 运动,当点 Q 到达点 D 时,点 Q 停止运动,设点 Q 运动的时间为 t 秒.
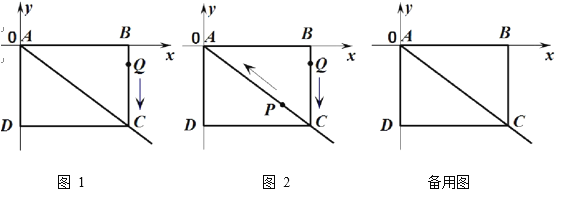
⑴请直接写出图 1 中,点 C 的坐标,并求出直线 OC 的表达式;
⑵求△ACQ 的面积 S 关于 t 的函数关系式,并写出 t 的取值范围;
⑶如图 2,当点 Q 开始运动时,点 P 从 C 点出发以每秒 2 个单位长度的速度运动向点 A运动,当点 P 到达 A 点时点 Q 和点 P 同时停止运动,当△QCP 与△ABC 相似时,求出相应的 t 值.
【答案】(1)(4,-3);![]() (2)
(2)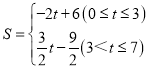 (3)
(3)![]() 或
或![]()
【解析】
(1)根据四边形是矩形及AB=4,AD=3可直接写成点 C 的坐标,并用待定系数法求出直线 OC 的表达式;
(2)分点Q在线段BC上及线段CD上两种情况讨论;
(3)先确定Q点的位置,再分![]() 和
和![]() 两种情况讨论.
两种情况讨论.
(1)根据题意得:
点 C 的坐标为(4,-3)
设直线 OC 的表达式为:y=kx
则-3=4k k=-![]()
∴直线 OC 的表达式为:![]()
(2)当点Q在线段BC上,即0≤t≤3时,
S=![]()
当点Q在线段CD上,即3<t≤7时,
![]()
∴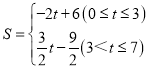
(3)∵四边形ABCD是矩形,AB=4,AD=3.
∴AC=5
∴P点从C点到A点需要2.5秒,则Q点在BC上运动
当△QCP∽ACB时,![]() ,
,
则![]() ,解得:
,解得:![]()
当△QCP∽BCA时,![]() ,
,
则![]() ,解得:
,解得:![]()
故当△QCP 与△ABC 相似时,![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).

(1)在图中作出△ABC的外接圆(保留必要的作图痕迹,不写作法),圆心坐标为 ______;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,且销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
(1)求证:∠BAE=∠CAD.
(2)若⊙O的半径为4,AC=5,CD=2,求CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0)的图象如图,给出下列4个结论:①abc>0; ②b2>4ac; ③4a+2b+c>0;④2a+b=0.其中正确的有( )个.
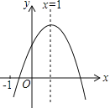
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=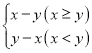 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
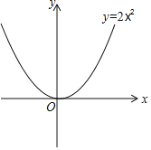
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
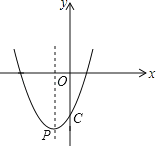
【题目】如图,已知二次函数![]() 的顶点P的横坐标为
的顶点P的横坐标为![]() ,且与y轴交于点C(0,-4).
,且与y轴交于点C(0,-4).
(1)求b,c的值;
(2)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧)点M关于y轴的对称点为点M,点H的坐标为(3,0).若四边形ONMH的面积为18.求点H到OM的距离;
(3)是否在对称轴的同侧存在实数m、n(m<n),当![]() 时,y的取值范围为
时,y的取值范围为![]() ?若存在,求出m,n的值;若不存在,说明理由.
?若存在,求出m,n的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com