
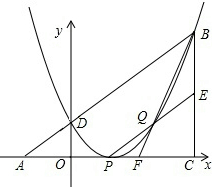
 已知Rt△ABC在平面直角坐标系中如图所示,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.
已知Rt△ABC在平面直角坐标系中如图所示,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.分析 (1)利用△ABC是等腰直角三角形,则△AOD也是等腰直角三角形,得出OD=OA,则D(0,m-3),AO=AC-OC=m-3;
(2)利用P(1,0)为抛物线顶点,可设顶点式,求解析式;
(3)设Q(x,x2-2x+1),过Q点分别作x轴,y轴的垂线,运用相似比求出FC、EC的长,而AC=m,代入即可.
解答 (1)解:由B(3,m)可知OC=3,BC=m,又△ABC为等腰直角三角形,
可得AC=BC=m,OA=m-3,
∵∠ODA=∠OAD=45°
∴OD=OA=m-3,
则点D的坐标是(0,m-3);
(2)解:∵抛物线顶点为P(1,0),且过点B、D,
∴可设抛物线的解析式为:y=a(x-1)2,
得:$\left\{\begin{array}{l}{a(3-1)^{2}=m}\\{a(0-1)^{2}=m-3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=1}\\{m=4}\end{array}\right.$
故抛物线的解析式为y=x2-2x+1;
(3)证明:如图所示:过点Q作QM⊥AC于点M,过点Q作QN⊥BC于点N,
设点Q的坐标是(x,x2-2x+1),
则QM=CN=(x-1)2,MC=QN=3-x.
∵QM∥CE
∴△PQM∽△PEC
∴$\frac{QM}{EC}$=$\frac{PM}{PC}$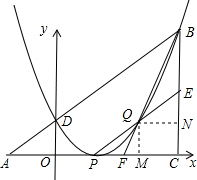
即$\frac{(x-1)^{2}}{EC}$=$\frac{x-1}{2}$,得EC=2(x-1)
∵QN∥FC
∴△BQN∽△BFC
∴$\frac{QN}{FC}$=$\frac{BN}{BC}$
即$\frac{3-x}{FC}$=$\frac{4-(x-1)^{2}}{4}$,得FC=$\frac{4}{x+1}$
又∵AC=4
∴FC(AC+EC)=$\frac{4}{x+1}$[4+2(x-1)]=$\frac{4}{x+1}$(2x+2)=$\frac{4}{x+1}$×2×(x+1)=8
即FC(AC+EC)为定值8.
点评 本题考查了点的坐标、抛物线解析式的求法、综合运用相似三角形的比求线段的长度,本题也可以先求直线PE、BF的解析式,利用解析式求FC,EC的长.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$+3 | C. | 4$\sqrt{3}$-3 | D. | 4$\sqrt{3}$+3或4$\sqrt{3}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 假设三个内角都不大于60° | B. | 假设三个内角都大于60° | ||
| C. | 假设三个内角至多有一个大于60° | D. | 假设三个内角至多有两个大于60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
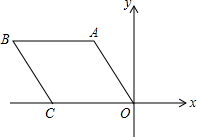 菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )
菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )| A. | (-2-$\sqrt{2}$,$\sqrt{2}$) | B. | (-2+$\sqrt{2}$,$\sqrt{2}$) | C. | (2+$\sqrt{2}$,$\sqrt{2}$) | D. | (2-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
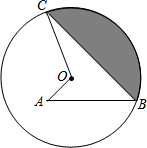 如图,已知点A为⊙O内一点,点B、C均在圆上,∠C=30°,∠A=∠B=45°,线段OA=$\sqrt{3}$-1,则阴影部分的周长为( )
如图,已知点A为⊙O内一点,点B、C均在圆上,∠C=30°,∠A=∠B=45°,线段OA=$\sqrt{3}$-1,则阴影部分的周长为( )| A. | $\frac{4π}{3}$+2$\sqrt{3}$ | B. | $\frac{2π}{3}$+2$\sqrt{3}$ | C. | $\frac{4π}{3}$+$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com