Question

【题目】在中，，于点，平分交于点，交于点，于点，连接．

（1）如图1，求证：四边形是菱形；

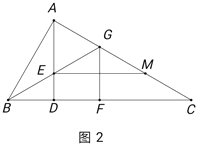
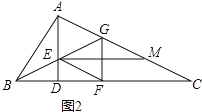
（2）如图2，若为的中点，过点作交于点，在不添加任何辅助线的情况下，请直接写出图2中是长倍的所有线段．

Answer 1

【答案】（1）证明见解析；（2）AB、BF、CF、EM．

【解析】

（1）先证明四边形AEFG是平行四边形，再证明AE=AG即可；

（2）先证明AB=AG，再分别证明AB=BF=CF=EM，CM=AG即可．

解：（1）∵AD⊥BC，GF⊥BC，

∴∠ADF=∠GFC=90°，

∴AE∥GF，

在△ABG和△FBG中， ，

∴△ABG≌△FBG，

∴AG=FG，

∵∠FBG+∠BED=90°，

∵∠BED=∠AEG，

∴∠FBG+∠AEG=90°，

∵∠ABG+∠AGE=90°，

∵∠ABG=∠FBG，

∴∠AEG=∠AGE，

∴AE=AG，

∴AE=FG，

∴四边形AEFG是平行四边形，

∵AE=AG∴四边形AEFG是菱形．
（2）∵四边形AEFG是菱形，

∴AE=AG，

∵BE=EG，∠BAG=90°，

∴AE=BE=EG，

∴△AEG是等边三角形，

∴∠AGE=60°，

在RT△ABG中，∵∠ABG=30°，

∴AB=AG，

∵∠C=30°，∴BC=2AB，

∴BE=GE，EF∥AC，EM∥BC，

∴BF=FC，CM=GM，

在RT△AEM中，∵∠AME=∠C=30°，∠GEM+∠GME=60°，

∴∠GEM=∠GME=30°，

∴EG=AG=GM=CM，

∵EM∥FC，EF∥CM，

∴四边形EFCM是平行四边形，

∴AB=BF=CF=EM=CM，

∴是CM长倍的所有线段有AB、BF、CF、EM．