
 如图,正方形OABC顶点AC分别在x轴y轴正半轴上A(m,0)且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解,OB=$\sqrt{2}$OA.
如图,正方形OABC顶点AC分别在x轴y轴正半轴上A(m,0)且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解,OB=$\sqrt{2}$OA.分析 (1)通过解分式方程求得m的值,易求正方形的边长,根据正方形的面积公式进行解答;
(2)利用角平分线的性质来求点D的坐标;
(3)由勾股定理来求OD的长度,利用面积法来求AE的长度,然后再由勾股定理来求DE的长度.
解答  解:(1)分式方程$\frac{2}{x}$=$\frac{3}{x+1}$得到:x=2.
解:(1)分式方程$\frac{2}{x}$=$\frac{3}{x+1}$得到:x=2.
经检验x=2是原方程的解,
所以A(0,2),
则OA=OC=2,
所以正方形OABC的面积是:2×2=4;
(2)设D(2,a).则AD=a,BD=2-a.
∵OD平分∠AOB
∴$\frac{OA}{AD}$=$\frac{OB}{BD}$,即$\frac{2}{a}$=$\frac{\sqrt{2}×2}{2-a}$,
解得a=$\sqrt{2}$-1.
故D(2,2$\sqrt{2}$-2).
(3)由(2)知,D(2,2$\sqrt{2}$-2).则由勾股定理得到OD=$\sqrt{O{A}^{2}+A{D}^{2}}$=$\sqrt{{2}^{2}+(2\sqrt{2}-2)^{2}}$=2$\sqrt{4-2\sqrt{2}}$.
由$\frac{1}{2}$OD•AE=$\frac{1}{2}$OA•AD得到:AE=$\frac{OA•AD}{OD}$=$\frac{2×(2\sqrt{2}-2)}{2\sqrt{4-2\sqrt{2}}}$=$\sqrt{2-\sqrt{2}}$.
在直角△AED中,由勾股定理得到:DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{(2\sqrt{2}-2)^{2}-2+\sqrt{2}}$=$\sqrt{10-7\sqrt{2}}$,
所以$\frac{AE+DE}{OD}$=$\frac{\sqrt{2-\sqrt{2}}+\sqrt{10-7\sqrt{2}}}{2\sqrt{4-2\sqrt{2}}}$=$\frac{\sqrt{(2-\sqrt{2})(4-2\sqrt{2})}+\sqrt{(10-7\sqrt{2})(4-2\sqrt{2})}}{2(4-2\sqrt{2})}$=$\frac{(\sqrt{2}-1)+(3-2\sqrt{2})}{2(2-\sqrt{2})}$=$\frac{1}{2}$.即$\frac{AE+DE}{OD}$=$\frac{1}{2}$.
点评 本题考查了四边形综合题,需要学生掌握正方形的性质,勾股定理,角平分线性质定理以及二次根式的化简.该题的计算量比较大,需要学生细心计算.


科目:初中数学 来源: 题型:选择题
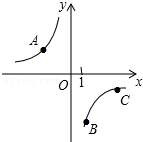 如图,A、B、C是反比例函数y=$\frac{k}{x}$(k<0)图象上三点,作直线l,使点A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
如图,A、B、C是反比例函数y=$\frac{k}{x}$(k<0)图象上三点,作直线l,使点A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校要征收一块土地,形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,土地价格为1 000元/m2,请你计算学校征收这块地需要多少钱?
学校要征收一块土地,形状如图所示,∠B=∠D=90°,AB=20m,BC=15m,CD=7m,土地价格为1 000元/m2,请你计算学校征收这块地需要多少钱?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com