
分析 (1)分类讨论:当k=0时,方程为以元一次方程,有解;当k≠0时,根据计算配不上得到△=(2k-1)2≥0,则可判断方程有两个实数解;
(2)利用求根公式得到x1=1+$\frac{1}{k}$,x2=3,则y=1-(1+$\frac{1}{k}$)=-$\frac{1}{k}$,于是可判断y是k的反比例函数.
解答 (1)证明:当k=0时,方程变形为-x+3=0,解得x=3;
当k≠0时,△=(4k+1)2-4k•(3k+3)=(2k-1)2≥0,方程有两个实数解,
所以不论k为何值,方程总有实数根;
(2)根据题意得x=$\frac{4k+1±(2k-1)}{2k}$,
所以x1=$\frac{k+1}{k}$=1+$\frac{1}{k}$,x2=3,
所以y=1-(1+$\frac{1}{k}$)=-$\frac{1}{k}$,
所以y是k的反比例函数.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
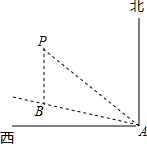 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
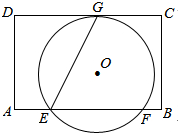 如图,在矩形ABCD中,AD=8,E是AB边上一点,且AE=$\frac{1}{4}$AB,⊙O经过点E,若⊙O与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在射线相交于另一点F,且EG:EF=$\sqrt{5}$:2.
如图,在矩形ABCD中,AD=8,E是AB边上一点,且AE=$\frac{1}{4}$AB,⊙O经过点E,若⊙O与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在射线相交于另一点F,且EG:EF=$\sqrt{5}$:2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )
如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com