
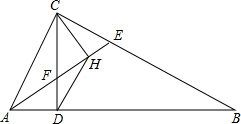
 △ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:
△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:分析 (1)根据余角的性质得到∠AFD=∠AEC,证得∠CFE=∠CEF,得到CF=CE,根据等腰三角形的性质即可得到结论.
(2)由于∠ADF=∠CHF=90°,∠AFD=∠CFH,得到△ADF∽△CFH,根据相似三角形的性质得到$\frac{CF}{AF}=\frac{HF}{DF}$,由于∠AFC=∠DFH,得到△AFC∽△DFH,根据相似三角形的性质得到∠CAF=∠CDH,等量代换即可得到结论.
解答 解:(1)∵∠ACB=90°,CD⊥AB于D,
∴∠CAE+∠AEC=∠DAF+∠AFD=90°,
∴∠AFD=∠AEC,
∵∠AFD=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE,
∵CH⊥EF,
∴HE=HF;
(2)∵∠ADF=∠CHF=90°,∠AFD=∠CFH,
∴△ADF∽△CFH,
∴$\frac{CF}{AF}=\frac{HF}{DF}$,
∵∠AFC=∠DFH,
∴△AFC∽△DFH,
∴∠CAF=∠CDH,
∵∠CAD=2∠CAF,
∴∠CAB=2∠CDH.
点评 本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:选择题
| A. | x<$\frac{5}{3}$ | B. | x>$\frac{5}{3}$ | C. | x<15 | D. | x>15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
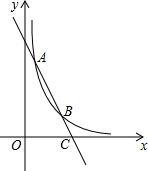 如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).
如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某新建小区要在一块的公共区修建一个圆形花坛,若要使花坛的面积最大,请你在这块区域内画出这个圆形花坛(使用直尺和圆规,不写画法,保留作图痕迹).
某新建小区要在一块的公共区修建一个圆形花坛,若要使花坛的面积最大,请你在这块区域内画出这个圆形花坛(使用直尺和圆规,不写画法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
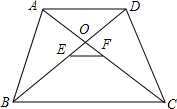 如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).
如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com