
分析 直接利用已知数据得出变化规律,进而得出答案.
解答 解:∵(1)$\sqrt{2+\frac{2}{3}}$=$2\sqrt{\frac{2}{3}}$;
(2)$\sqrt{3+\frac{3}{8}}$=$3\sqrt{\frac{3}{8}}$;
(3)$\sqrt{4+\frac{4}{15}}$=$4\sqrt{\frac{4}{15}}$;
(4)$\sqrt{5+\frac{5}{24}}=5\sqrt{\frac{4}{25}}$
∴用含有n(n是正整数,且n>1)的代数式将规律表示出来为:$\sqrt{a+\frac{a}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$.
故答案为:$\sqrt{a+\frac{a}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$.
点评 此题主要考查了二次根式的性质与化简,正确得出数字之间变化规律是解题关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥0 | B. | a≤1 | C. | 0≤a≤1 | D. | a>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
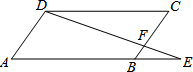 如图,E是?ABCD边AB延长线上的一点,AB=4BE,连接DE交BC于点F,则△DCF与四边形ABFD面积的比是$\frac{2}{3}$.
如图,E是?ABCD边AB延长线上的一点,AB=4BE,连接DE交BC于点F,则△DCF与四边形ABFD面积的比是$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com