
| A. | a≥0 | B. | a≤1 | C. | 0≤a≤1 | D. | a>1 |
分析 由于二次函数的顶点坐标不能确定,故应分对称轴不在[1,5]和对称轴在[1,5]内两种情况进行解答.
解答 解:第一种情况:
当二次函数的对称轴不在1≤x≤5内时,此时,对称轴一定在1≤x≤5的左边,函数方能在这个区域取得最大值,
x=$\frac{2-a}{2}$≤1,即a≥0,
第二种情况:
当对称轴在1≤x≤5内时,对称轴一定是在区间1≤x≤5的中点的左边,因为如果在中点的右边的话,就是在x=5的地方取得最大值,即:
x=$\frac{2-a}{2}$≤$\frac{1+5}{2}$,即a≥-4,
综合上所述a≥0.
故选A.
点评 本题考查了二次函数的最值确定与自变量x的取值范围的关系,难度较大.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | C>A>B | B. | B>A>C | C. | C>B>A | D. | B>C>A |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,面积为5的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,已知点B的坐标是(1,3),则k的值为( )
如图,面积为5的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,已知点B的坐标是(1,3),则k的值为( )| A. | 16 | B. | 12 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
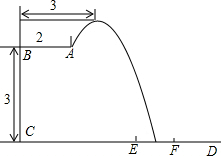 2016年跳水世界杯,于2月19日至24日在巴西里约举行,中国队取得佳绩.优秀成绩的取得离不开艰辛的训练,某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,BC为纵轴建立直角坐标系.
2016年跳水世界杯,于2月19日至24日在巴西里约举行,中国队取得佳绩.优秀成绩的取得离不开艰辛的训练,某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,BC为纵轴建立直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com