
 ��ͼ����֪��ABC�У���B=90�㣬AB=8cm��BC=6cm��P��Q�ǡ�ABC���ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊt�룮
��ͼ����֪��ABC�У���B=90�㣬AB=8cm��BC=6cm��P��Q�ǡ�ABC���ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊt�룮���� ��1�����ݵ�P��Q���˶��ٶ����AP�������BP��BQ���ù��ɶ������PQ���ɣ�
��2���ɹ��ɶ������AC��������ó����̣��ⷽ�����t�����ɵó����ۣ�
��3������Q�ڱ�CA���˶�ʱ����ʹ��BCQ��Ϊ���������ε��˶�ʱ�������������
�ٵ�CQ=BQʱ��ͼ1�������C=��CBQ����֤����A=��ABQ����BQ=AQ����CQ=AQ���Ӷ����t��
�ڵ�CQ=BCʱ��ͼ2������BC+CQ=12�������t��
�۵�BC=BQʱ��ͼ3������B����BE��AC�ڵ�E�������BE��CE�����ɵó�t��
��� �⣺��1��BQ=2��2=4cm��
BP=AB-AP=8-2��1=6cm��
�ߡ�B=90�㣬
��PQ=$\sqrt{B{Q}^{2}+B{P}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$��
��2���ɹ��ɶ����ã�AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10��cm����
��������ã�BQ=2tcm��CQ=��6-2t��cm��PA=tcm��BP=��8-t��cm��
��PQ�ܰѡ�ABC���ܳ�ƽ�֣���BQ+BP=CQ+PA+AC��
��2t+8-t=6-2t+t+10��
��ã�t=4��
��ʱCQ=6-2t=-2��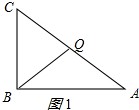
��t=4�������⣬
���Q�ڱ�BC���˶�ʱ��ͨ������PQ���ܰѡ�ABC���ܳ�ƽ�֣�
��3���ٵ�CQ=BQʱ����ͼ1��ʾ��
���C=��CBQ��
�ߡ�ABC=90�㣬
���CBQ+��ABQ=90�㣬
��A+��C=90�㣬
���A=��AB
��BQ=AQ��
��CQ=AQ=5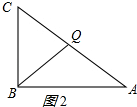
��BC+CQ=11��
��t=11��2=5.5�룮
�ڵ�CQ=BCʱ����ͼ2��ʾ��
��BC+CQ=12
��t=12��2=6�룮
�۵�BC=BQʱ����ͼ3��ʾ��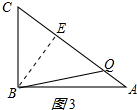
��B����BE��AC�ڵ�E��
��BE=$\frac{AB•BC}{AC}$=$\frac{6��8}{10}$=4.8��cm��
��CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=3.6cm��
��CQ=2CE=7.2cm��
��BC+CQ=13.2cm��
��t=13.2��2=6.6�룮
���Ͽ�֪����tΪ5.5���6���6.6��ʱ��
��BCQ����������
���� ���⿼���˹��ɶ����������ε�����Լ����������ε��ж������ʣ�������һ���Ѷȣ�ע���������˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
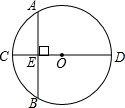 ��֪����O�İ뾶Ϊ6cm����AB��ֱ��CD��ֱ���ҽ�CD�ֳ�1��3�����֣�����AB�ij���
��֪����O�İ뾶Ϊ6cm����AB��ֱ��CD��ֱ���ҽ�CD�ֳ�1��3�����֣�����AB�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
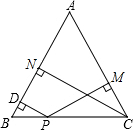 ��ͼ���ڡ�ABC�У�AB=AC��PΪBC��һ�㣬PD��AB�ڵ�D��PM��AC�ڵ�M��CNΪ�ߣ���AC=8��S��ABC=20����PD+PM��ֵ��
��ͼ���ڡ�ABC�У�AB=AC��PΪBC��һ�㣬PD��AB�ڵ�D��PM��AC�ڵ�M��CNΪ�ߣ���AC=8��S��ABC=20����PD+PM��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
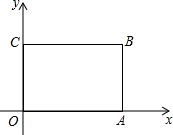 ��ͼ������OABC�Ķ�������ֱ�ΪO��0��0����A��6��0����B��6��4����C��0��4���������Ե�OΪλ�����ģ�����OABC��λ��ͼ��O��A��B��C�䣬ʹ����������ھ���OABC�����$\frac{1}{4}$�����ֱ�д����A�䣬B�䣬C������꣮
��ͼ������OABC�Ķ�������ֱ�ΪO��0��0����A��6��0����B��6��4����C��0��4���������Ե�OΪλ�����ģ�����OABC��λ��ͼ��O��A��B��C�䣬ʹ����������ھ���OABC�����$\frac{1}{4}$�����ֱ�д����A�䣬B�䣬C������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com