
已知:如图1,Rt△ABC中,∠BAC=90°,点D是线段AC的中点,连接BD并延长至点E,使BE=2BD.连接AE,CE.
(1)求证:四边形ABCE是平行四边形;
(2)如图2所示,将三角板顶点M放在AE边上,两条直角边分别过点B和点C,若∠MEC=∠EMC,BM交AC于点N.
①求证:△ABN≌△MCN;
②当点M恰为AE中点时sin∠ABM= .


【考点】四边形综合题.
【分析】(1)先证BD=DE,再加上AD=DC的条件可直接得出结论;
(2)①先CM=CE=BA,然后由“角角边”定理直接得出结论;
②由M是AE中点,得出CM=EM=AM,再结合CE=CM,可证得△CEM是等边三角形,从而∠CMA=∠ABM=30°.
【解答】解:(1)∵点D是线段AC的中点,BE=2BD,
∴AD=CD,DE=BD,
∴四边形ABCE是平行四边形.
(1)①∵四边形ABCE是平行四边形,
∴CE=AB,
∵∠MEC=∠EMC,
∴CM=AB,
在△ABN和△MCN中,
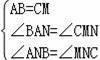
 ,
,
∴△ABN≌△MCN(AAS);
②∵∠ACE=∠CAB=90°,M为AE中点,
∴CM=EM=AM,
∵CE=CM,
∴CE=CM=EM,
∴△CEM是等边三角形,
∴∠CME=2∠MCA=60°,
∴∠MCA=30°,
∵△ABN≌△MCN,
∴∠ABM=∠MCA=30°,
∴sin∠ABM=
 .
.
【点评】本题为四边形综合题,主要考查了平行四边形的判定与性质、全等三角形的判定与性质、直角三角形斜边中线定理、等边三角形的判定与性质、特殊角的三角函数等知识点,难度不大,属中档题.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
下列说法正确的是( )
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直的四边形是菱形
D.有一个角是直角的平行四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
国务院总理李克强在第十二届全国人大第四次政府工作报告中指出,2015年我国国内生产总值达到了67.7万亿元,67.7万亿元用科学记数法表示为( )
A.67.7×1012 B.6.77×1013 C.0.677×1014 D.6.77×1014
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中逆命题是真命题的是( )
A.对顶角相等
B.若两个角都是45°,那么这两个角相等
C.全等三角形的对应角相等
D.两直线平行,同位角相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com