
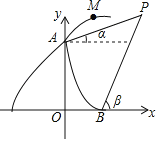
����Ŀ����ͼ��ij�������䳵��ɽ��A���������ѵ����ʾ��ͼ����A��y���ϣ���ԭ��O�ľ�����8���ף�Ϊ�˼��㷽�㣬���ǰѱ����еľ����ð�������λ�����˵������䳵��A������ij���Ƕȵ����ѵ������M�ǵ��������������ijʱ�̵�λ�ã����Կ���������ʵ��������������t��ʱ����M��A��ˮƽ������vt���ף���M��x�ᣨˮƽ������ֱ�����ǣ�8+vt��5t2�����ף�v��ֵ�ɷ������趨�����ڵ�A��x���ϵĵ�B���۲����Ŀ��P�����Ƿֱ���a������OB��3���ף�tan����![]() ��tan����
��tan����![]() ��
��
��1����v��7������������⣺
������M��A��ˮƽ������7����ʱ����M��x��ľ������� �����ף�
�����M����Ϊ��x��y������y��x�Ĺ�ϵʽ������дx��ȡֵ��Χ����
��2������1���������ʽ���ܷ�����Ŀ��P����˵�����ɣ�
��3��Ŀ����m����/����ٶȴӵ�P�����ƶ�����v![]() ʱ������ʹĿ�걻���У���m��ȡֵ��Χ��
ʱ������ʹĿ�걻���У���m��ȡֵ��Χ��
���𰸡���1����10����y����![]() ����2���ܣ����ɼ���������3��0��m��
����2���ܣ����ɼ���������3��0��m��![]() ��
��
��������
��1���ٸ���ˮƽ������7����֪��vt��7����v��7�����t��1���ٴ����M��x�ᣨˮƽ������ֱ�����ǣ�8+vt��5t2�������У��ɵý��ۣ�
�ڸ��ݵ�M����Ϊ��x��y��������֪��M��vt��8+vt��5t2����v��7�����з�����ɵý��ۣ�
��2�������P�����꣬���������ߵĽ���ʽ��������������Ŀ��P��
��3���ɣ�2��֪��7��v��6![]() ����v�����ֵ����M�ĺ��������б�ʾ��y��x�Ĺ�ϵʽ���ɣ�2��֪��P��7��10��������P��������ƽ�ƣ���P�������겻�䣬����10������ɵ�x��ֵ������ʱ�䣬�Ӷ��ý��ۣ�
����v�����ֵ����M�ĺ��������б�ʾ��y��x�Ĺ�ϵʽ���ɣ�2��֪��P��7��10��������P��������ƽ�ƣ���P�������겻�䣬����10������ɵ�x��ֵ������ʱ�䣬�Ӷ��ý��ۣ�
��1���ٵ�v��7ʱ��vt��7��
��7t��7��t��1��
��8+vt��5t2��8+7��1��5��12��15��5��10��
�ʴ�Ϊ��10��
�ڡߵ�M����Ϊ(x��y)��
������ã�M(vt��8+vt��5t2)��v��7����
��![]() ,
,
��t��![]() x��
x��
��y����![]() ��
��
��2���ܣ��������£�
��PC��x���ڵ�C��AD��PC�ڵ�D����ͼ��ʾ��
��OC��AD��a����BC��a��3��
��tan����![]() ��tan����
��tan����![]() ���ã�PD��
���ã�PD��![]() a��PC��
a��PC��![]() ��a��3����
��a��3����
��PC��PD��8����![]() ��a��3����
��a��3����![]() a��8��
a��8��
��ã�a��7����PC��![]() ����7��3����10��
����7��3����10��
���P������Ϊ(7��10)��
��x��7ʱ��y����![]() ��10��
��10��
�������߹���P����������Ŀ��P��
��3��������ã�v��ֵԽ���ڵ��������ԽԶ������Խ����Ŀ�꣬
�ɣ�2��֪��7��v��6![]() ��
��
��v��6![]() ʱ��x��6
ʱ��x��6![]() t��y��8+6
t��y��8+6![]() t��5t2����y����
t��5t2����y����![]() x2+x+8��
x2+x+8��
��Ŀ�������ƶ���y��10������![]() x2+x+8=10��
x2+x+8=10��
��ã�x1��12��x2��![]() ���ᣩ��
���ᣩ��
�൱y��10ʱ���ڵ�������Զ���12���ף���ʱ��![]() ��
��![]() ��
��![]() ���룩��
���룩��
��![]() m��12��7����m��
m��12��7����m��![]() ��
��
��0��m��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
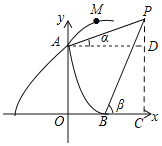
����Ŀ����ͼ����![]() �Ƿ���������
�Ƿ���������![]() ͼ���ϵ����㣨��
ͼ���ϵ����㣨��![]() �ڵ�
�ڵ�![]() ��ࣩ������
��ࣩ������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֪
����֪![]() ��
��![]() ����
����![]() ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
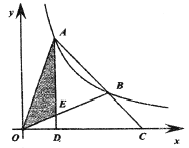
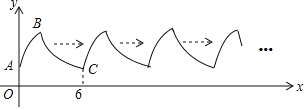
����Ŀ����ͼ������AB�Ƕ���ΪB����y�ύ�ڵ�A��������y����x2+4x+2��һ���֣�����BC��˫����y��![]() ��һ���֣��ɵ�C��ʼ�����ظ���A��B��C���Ĺ��̣��γ�һ�鲨���ߣ���P��2018��m����Q��2026��n�����ڸ��������ϣ���m+n��_____��
��һ���֣��ɵ�C��ʼ�����ظ���A��B��C���Ĺ��̣��γ�һ�鲨���ߣ���P��2018��m����Q��2026��n�����ڸ��������ϣ���m+n��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������һ����ֹ�Ĺ������C���ӵ���A����C�������Ϊ45�����ӵ���B����C�������Ϊ60������֪AB��20m����C��ֱ��AB��ͬһǦ��ƽ���ϣ������������ĸ߶ȣ�����������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
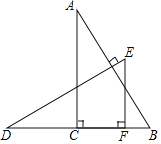
����Ŀ����ͼ����ABC�͡�DEF����ֱ�������Σ���ACB����DFE��90�㣬AB��DE������F��BC�ϣ���DF������C����A��E��BCͬ�࣬DE��AB��
��1����֤����ABC�ա�DEF��
��2����AC��11��EF��6��CF��4����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ�����O��BD����O��ֱ����AE��CD�ڵ�E��DAƽ����BDE
��������֤��AE����O�����ߣ�
����������DBC=30����DE=1 cm����BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
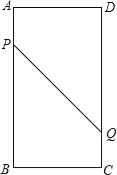
����Ŀ����ͼ���ھ���ABCD�У�AB��16cm��BC��6cm����P�ӵ�A������AB��3cm/s���ٶ����B�ƶ��������A��B�غϣ���ͬʱ��Q�ӵ�C������CD��2cm/s���ٶ����D�ƶ��������C��D�غϣ����������룬��PDQΪֱ�������Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BOC��140����I�����ģ�O�����ģ����BIC���ڣ� ��

A.130��B.125��C.120��D.115��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
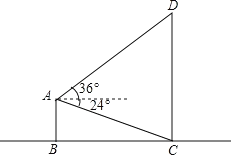
����Ŀ����ͼ��AB��CD���Ǵ�ֱ�ڵ���BC�Ľ�����ڽ�����AB�Ķ���A����ý�����CD�ĵ�C�ĸ���Ϊ24�㣬��ö���D������Ϊ36�㣬��AC=200�ף�AD=300�ף�������CD�ĸ߶ȣ�(�����������)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com