练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

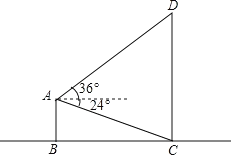
    【题目】如图，AB与CD都是垂直于地面BC的建筑物．在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°，测得顶端D的仰角为36°，若AC=200米，AD=300米，求建筑物CD的高度．(结果保留根号)

    【答案】(300sin36°+200sin24°)米．

    【解析】

    过点A作AE⊥CD后，图中将有两个直角三角形．先在Rt△ADE中，利用已知角的正弦值求出CE；然后在Rt△CEA中，利用已知角的正弦值求出CE即可解决问题．

    过点A作AE⊥CD，垂足为E．

    在Rt△ADE中，有DE=AD×sin36°=300sin36°米；

    在Rt△ACE中，可得CE=AC×sin24°=200sin24°米．

    故CD=DE+EC=(300sin36°+200sin24°)米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

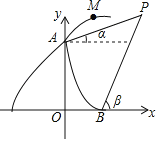
    【题目】如图是某导弹发射车在山顶A处进行射击训练的示意图，点A在y轴上，与原点O的距离是8百米（为了计算方便，我们把本题中的距离用百米作单位）．此导弹发射车在A处进行某个角度的射击训练，点M是导弹向右上射出后某时刻的位置．忽略空气阻力，实验表明：导弹射出t秒时，点M，A的水平距离是vt百米，点M与x轴（水平）的竖直距离是（8+vt﹣5t2）百米（v的值由发射者设定）．在点A和x轴上的点B处观测射击目标P的仰角分别是a和β，OB＝3百米，tanα＝．tanβ＝．

    （1）若v＝7，完成下列问题：

    ①当点M，A的水平距离是7百米时，点M到x轴的距离是　 　百米；

    ②设点M坐标为（x，y），求y与x的关系式（不必写x的取值范围）．

    （2）按（1）的射击方式，能否命中目标P？请说明理由．

    （3）目标以m百米/秒的速度从点P向右移动，当v时，若能使目标被击中，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，AD是⊙O的弦，BC是⊙O的切线，切点为B．

    （1）求证：；

    （2）若AB＝5，AD＝8，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

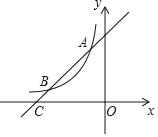
    【题目】如图，一次函数y＝x+4的图象与反比例函数y＝(k为常数且k≠0)的图象交于A(﹣1，a)，B两点，与x轴交于点C．

    (1)求a，k的值及点B的坐标；

    (2)若点P在x轴上，且S△ACP＝S△BOC，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB、BC、CD分别与⊙O相切于E、F、G三点，且AB∥CD，OB＝6cm，OC＝8cm．

    （Ⅰ）求证：OB⊥OC；

    （Ⅱ）求CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某厂计划生产A、B两种产品共100件，已知A产品每件可获利润400元，B产品每件可获利润500元，其中规定生产B产品的数量不超过A产品数量的2倍，设生产A产品的数量为x(件)，生产两种产品的获利总额为y(元)

    （1）写出y与x之间的函数表达式；

    （2）该厂生产A、B两种产品各多少台，才能使获利总额最大？最大利润是多少？

    （3）在实际生产过程中，A产品生产成本下降了m(0＜m＜200)元且最多生产60件，B产品生产成本不变，请根据以上信息，设计出该厂生产100件A、B两种产品获利最多的生产方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

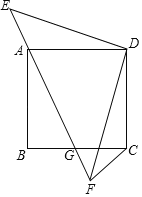
    【题目】如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．

    ①求证：△DAE≌△DCF；

    ②求证：△ABG∽△CFG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

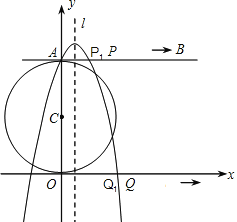
    【题目】如图，在平面直角坐标系中，以点C(0，4)为圆心，半径为4的圆交y轴正半轴于点A，AB是⊙C的切线．动点P从点A开始沿AB方向以每秒1个单位长度的速度运动，点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动，且动点P、Q从点A和点O同时出发，设运动时间为t(秒)．

    （1）当t＝1时，得到P1、Q1，求经过A、P1、Q1三点的抛物线解析式及对称轴l；

    （2）当t为何值时，直线PQ与⊙C相切？并写出此时点P和点Q的坐标；

    （3）在(2)的条件下，抛物线对称轴l上存在一点N，使NP＋NQ最小，求出点N的坐标并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上．

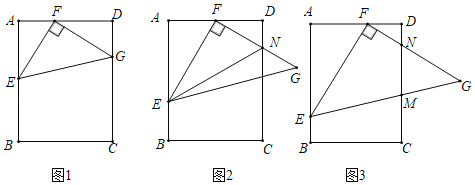
    （1）如图1，当点G在CD上时，求证：△AEF≌△DFG；

    （2）如图2，若F是AD的中点，FG与CD相交于点N，连接EN，求证：EN＝AE+DN；

    （3）如图3，若AE＝AD，EG，FG分别交CD于点M，N，求证：MG2＝MNMD.

    查看答案和解析>>

    同步练习册答案