
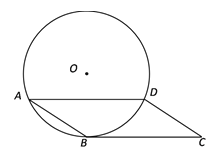
【题目】如图,在□ABCD中,AD是⊙O的弦,BC是⊙O的切线,切点为B.
(1)求证:![]() ;
;
(2)若AB=5,AD=8,求⊙O的半径.
【答案】(1)证明见解析;(2)⊙O的半径为![]()
【解析】
(1) 连接OB,根据题意求证OB⊥AD,利用垂径定理求证;
(2) 根据垂径定理和勾股定理求解.
解:(1)

连接OB,交AD于点E.
∵BC是⊙O的切线,切点为B,
∴OB⊥BC.
∴∠OBC=90°
∵ 四边形ABCD是平行四边形
∴AD// BC
∴∠OED=∠OBC =90°
∴ OE⊥AD
又 ∵ OE过圆心O
∴ ![]()
(2)∵ OE⊥AD ,OE过圆心O
∴ AE=![]() AD=4
AD=4
在Rt△ABE中,∠AEB=90°,
BE=![]() =3,
=3,
设⊙O的半径为r,则OE=r-3
在Rt△ABE中,∠OEA=90°,
OE2+AE2 = OA2
即(r-3)2+42= r2 ∴r=![]()
∴⊙O的半径为![]()


科目:初中数学 来源: 题型:
【题目】我市倡导垃圾分类投放,将日常垃圾分成四类,分别投放四种不同颜色的垃圾桶中,在“垃圾分类”模拟活动中,某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中,则这个同学正确分类投放垃圾的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.
(1)若售价下降1元,每月能售出 个台灯,若售价下降x元(![]() ),每月能售出 个台灯.
),每月能售出 个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)月获利能否达到9600元,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
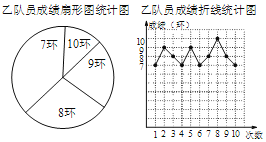
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员单行了一次选拔赛,要求这两名队员各射击10次,比赛结束后,根据比赛成绩情况,将甲,乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表:
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 3 | 1 |
(1)在乙队员成绩扇形统计图中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表:
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | 8 | b | 1 |
求表中的a、b、c的值(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿着折线
的速度沿着折线![]() 运动,到达点
运动,到达点![]() 时停止运动;点
时停止运动;点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿着折线
的速度沿着折线![]() 运动,到达点
运动,到达点![]() 时停止运动.点
时停止运动.点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
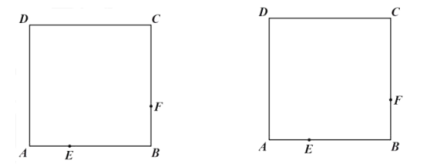
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
(2)连接![]() 、
、![]() 交与点
交与点![]() ,
,
①在整个运动过程中,![]() 的最小值为______
的最小值为______![]() ;
;
②当![]() 时,此时
时,此时![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
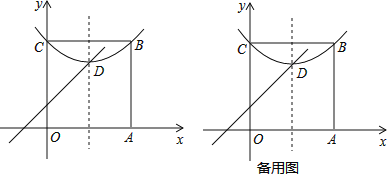
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫做该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A,C分别在x轴和y轴上,抛物线y=![]() (x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
(x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取![]() ,计算结果保留一位小数)
,计算结果保留一位小数)

(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com