
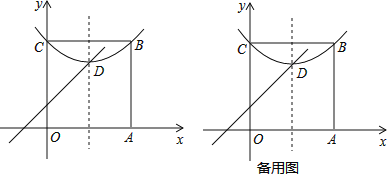
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫做该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A,C分别在x轴和y轴上,抛物线y=![]() (x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
(x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
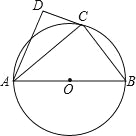
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若整数a既使关于x的分式方程![]() ﹣
﹣![]() =1的解为非负数,又使不等式组
=1的解为非负数,又使不等式组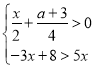 有解,且至多有5个整数解,则满足条件的a的和为( )
有解,且至多有5个整数解,则满足条件的a的和为( )
A.﹣5B.﹣3C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①b=2a;②c﹣a=n;③抛物线另一个交点(m,0)在﹣2到﹣1之间;④当x<0时,ax2+(b+2)x<0;⑤一元二次方程ax2+(b﹣![]() )x+c=0有两个不相等的实数根其中正确结论的个数是( )
)x+c=0有两个不相等的实数根其中正确结论的个数是( )
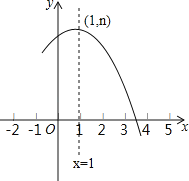
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,建立如图所示的平面直角坐标系xOy,ΔABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
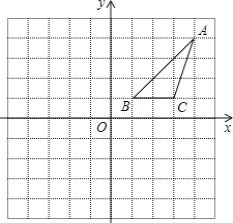
(1)画出ΔABC关于y轴对称的ΔA1B1C1,并写出点A1,B1,C1的坐标;
(2)将ΔABC绕点C逆时针旋转90°,画出旋转后的ΔA2B2C,并写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)BF和DE有怎样的数量关系?请证明你的结论;
(2)在其他条件都保持不变的是情况下,当点E运动到AC中点时,四边形AFBE是什么特殊四边形?请证明你的结论.
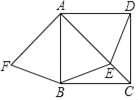
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2ax+m的图象经过点P(4,5),与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,且S△PAB=10.
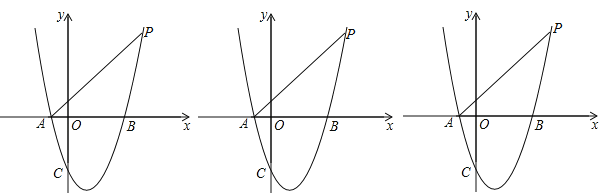
(1)求抛物线的解析式;
(2)在抛物线上是否存在点Q使得△PAQ和△PBQ的面积相等?若存在,求出Q点的坐标,若不存在,请说明理由;
(3)过A、P、C三点的圆与抛物线交于另一点D,求出D点坐标及四边形PACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:如果二次函数![]() 的图像经过点(-1,0),那么称此二次函数的图像为“定点抛物线”
的图像经过点(-1,0),那么称此二次函数的图像为“定点抛物线”
(1)试判断二次函数![]() 的图像是否为“定点抛物线”
的图像是否为“定点抛物线”
(2)若定点抛物线![]() 与x轴只有一个公共点,求
与x轴只有一个公共点,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com