
【题目】如图,抛物线y=ax2﹣2ax+m的图象经过点P(4,5),与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,且S△PAB=10.
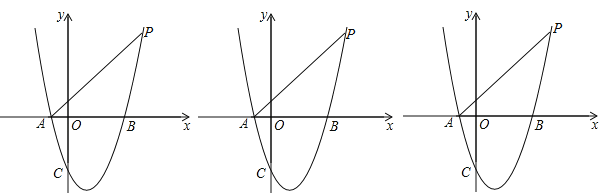
(1)求抛物线的解析式;
(2)在抛物线上是否存在点Q使得△PAQ和△PBQ的面积相等?若存在,求出Q点的坐标,若不存在,请说明理由;
(3)过A、P、C三点的圆与抛物线交于另一点D,求出D点坐标及四边形PACD的周长.
【答案】(1)y=x2﹣2x﹣3;(2)点Q的坐标为:(﹣2,5)或(﹣![]() ,﹣
,﹣![]() );(3)6
);(3)6![]() +4
+4![]() .
.
【解析】
(1)因为抛物线y=ax2﹣2ax+m,函数的对称轴为:x=1,S△PAB=10=![]() ×AB×yP=
×AB×yP=![]() AB×5,解得AB=4,即可求解;(2)分A、B在点Q(Q′)的同侧;点A、B在点Q的两侧两种情况,分别求解即可;(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,故圆O′是过A、P、C三点的圆,即可求解.
AB×5,解得AB=4,即可求解;(2)分A、B在点Q(Q′)的同侧;点A、B在点Q的两侧两种情况,分别求解即可;(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,故圆O′是过A、P、C三点的圆,即可求解.
解:
(1)y=ax2﹣2ax+m,函数的对称轴为:x=1,
S△PAB=10=![]() ×AB×yP=
×AB×yP=![]() AB×5,解得:AB=4,
AB×5,解得:AB=4,
故点A、B的坐标分别为:(﹣1,0)、(3,0),
抛物线的表达式为:y=a(x+1)(x﹣3),
将点P的坐标代入上式并解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3…①;
(2)①当A、B在点Q(Q′)的同侧时,如图1,
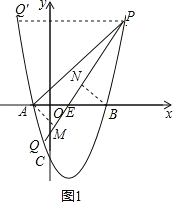
△PAQ′和△PBQ′的面积相等,则点P、Q′关于对称轴对称,
故点Q′(﹣2,5);
②当A、B在点Q的两侧时,如图1,
设PQ交x轴于点E,分别过点A、B作PQ的垂线交于点M、N,
△PAQ和△PBQ的面积相等,则AM=BN,
而∠BEN=∠AEM,∠AME=∠BNE=90°,
∴△AME≌△BNE(AAS),
∴AE=BE,
即点E是AB的中点,则点E(1,0),
将点P、E的坐标代入一次函数表达式并解得:
直线PQ的表达式为:y=![]() x﹣
x﹣![]() …②,
…②,
联立①②并解得:x=﹣![]() 或4(舍去4),
或4(舍去4),
故点Q(﹣![]() ,﹣
,﹣![]() ),
),
综上,点Q的坐标为:(﹣2,5)或(﹣![]() ,﹣
,﹣![]() );
);
(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,
故圆O′是过A、P、C三点的圆,
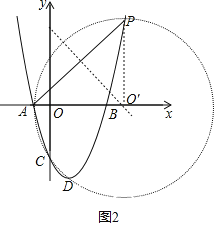
设点D(m,m2﹣2m﹣3),点O′(4,0),则DO′=5,
即(m﹣4)2+(m2﹣2m﹣3)2=25,
化简得:m(m+1)(m﹣1)(m﹣4)=0,
解得:m=0或﹣1或1或4(舍去0,﹣1,4),
故:m=1,
故点D(1,﹣4);
四边形PACD的周长=PA+AC+CD+PD=![]() .
.


科目:初中数学 来源: 题型:
【题目】某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.
(1)若售价下降1元,每月能售出 个台灯,若售价下降x元(![]() ),每月能售出 个台灯.
),每月能售出 个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)月获利能否达到9600元,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
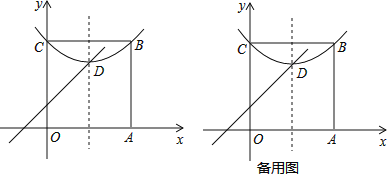
【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫做该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A,C分别在x轴和y轴上,抛物线y=![]() (x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
(x﹣a)2+b经过B,C两点,顶点D在正方形内部.若点D有一条特征线是y=x+2,则此抛物线的表达式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象经过点
的图象经过点![]() ,
,![]() .
.
(1)求代数式mn的值;
(2)若二次函数![]() 的图象经过点B,求代数式
的图象经过点B,求代数式![]() 的值;
的值;
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象只有一个交点,且该交点在直线
的图象只有一个交点,且该交点在直线![]() 的下方,结合函数图象,求
的下方,结合函数图象,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取![]() ,计算结果保留一位小数)
,计算结果保留一位小数)

(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com