练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

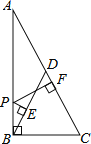
    【题目】如图．在Rt△ABC中，∠ABC=90°，点D是斜边上的中点，点P在AB上，PE⊥BD于E，PF⊥AC于F，若AB=6，BC=3，则PE+PF=（　　）

    A.

    B.

    C.

    D.

    【答案】A

    【解析】

    如图作BM⊥AC于M，连接PD，根据勾股定理可求得AC的长，再根据直角三角形斜边中线的性质可得BD=AD=DC，利用面积法可求得BM的长，再根据S△ABD=S△ADP+S△BDP，即可求得PE+PF的长.

    如图作BM⊥AC于M，连接PD，

    ∵∠ABC=90°，AD=DC，AB=6，BC=3，

    ∴BD=AD=DC，AC= ,

    ∵ ABBC=ACBM，

    ∴BM=，

    ∴S△ABD=S△ADP+S△BDP，

    ∴ADBM=ADPF+BDPE，

    ∴PE+PF=BM=，

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=8，AD=6，P为射线AB上一个动点，过P作PF⊥AC，垂足为F，交CD于点G，连接CP与BF交于点H，过点C，P，F作⊙O．

    （1）当AP=5时，求证：∠CPB=∠FBC．

    （2）当点P在线段AB上时，若△FCH的面积等于△PBH面积的4倍，求DG的长．

    （3）当⊙O与△ADC的其中一边相切时，求所有满足条件的AP的长．

    （4）当H将线段CP分成1：4的两部分时，求AP的长(直接写出结果)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年初，受新冠肺炎疫情的影响，全国各中小学都采取了线上学习方式．为了解九年级学生网上学习的效果，甲、乙两个学校同时参加了一次相同的网上测试，记录成绩（百分制）．分别从甲、乙两所学校随机抽取了20名学生的测试成绩，数据如下（百分制）：

    甲：63 70 95 84 75 82 78 78 86 96

    92 100 52 89 88 84 84 92 90 84

    乙：75 95 85 93 85 92 84 89 96 98

    46 86 77 100 100 68 50 85 78 69

    整理上面的数据，得到表格如下：

    测试成绩（分）

    甲

    1

    2

    3

    9

    5

    乙

    2

    2

    3

    6

    7

    样本数据的平均数、中位数、众数如下表所示：

    统计量

    平均数

    中位数

    众数

    甲

    83.1

    84

    乙

    82.4

    85.5

    根据以上信息，解答下列问题：

    （1）表中的 ， ；

    （2）若甲学校共有500名学生，请用样本中的数据估计甲学校共有多少人的测试成绩达到优秀（规定：测试成绩分为优秀）；

    （3）根据以上数据推断一所你认为成绩较好的学校，并说明理由．（至少从两个不同的角度结合数据说明推断的合理性）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在春季“植树节”活动中，王亮和李明两位同学想通过摸球的方式来决定谁去参加学校的植树节活动，规则如下：在两个盒子内分别装入标有数字1，2，3，4的四个和标有数字1，2，3的三个完全相同的小球，分别从两个盒子中摸出一个小球，如果所摸出的小球上的数字之和小于6，那么王亮去，否则就是李明去．

    （1）用画树状图或列表的方法，求出王亮去的概率；

    （2）李明说：“这种规则不公平”，你认同他的说法吗？请你说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y＝ax2＋bx＋c(a≠0)的部分图象，其顶点坐标为(1，n)，抛物线与x轴的一个交点在点(3，0)和(4，0)之间．则下列结论

    ①a－b＋c＞0；②3a＋b＝0；

    ③b2＝4a(c－n)；

    ④一元二次方程ax2＋bx＋c＝n－1有两个不相等的实数根．

    其中正确结论的个数是(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A（3，1），B（1，0），PQ是直线y=x上的一条动线段且PQ=（Q在P的下方），当AP+PQ+QB取最小值时，点Q坐标为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

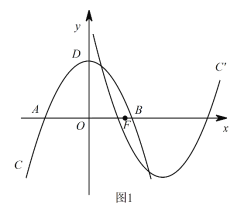
    【题目】如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D(0，4)，AB=4，设点F(m，0)是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C/．

    (1)求抛物线C的函数表达式；

    (2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．

    (3)如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线C/上的对应点P/，设M是C上的动点，N是C/上的动点，试探究四边形PMP/N能否成为正方形？若能，请直接写出m的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

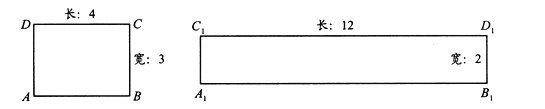
    【题目】阅读理解：给定一个矩形，如果存在另一个矩形，它的周长和面积分别是已知矩形的周长和面积的2倍，则这个矩形是给定矩形的“加倍”矩形.如图，矩形是矩形的“加倍”矩形.

    解决问题：

    （1）当矩形的长和宽分别为3，2时，它是否存在“加倍”矩形？若存在，求出“加倍”矩形的长与宽，若不存在，请说明理由.

    （2）边长为的正方形存在“加倍”正方形吗？请做出判断，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

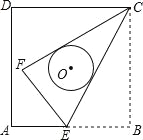
    【题目】如图，正方形ABCD的边长为4，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE的长为 ．

    查看答案和解析>>

    同步练习册答案