
【题目】2020年初,受新冠肺炎疫情的影响,全国各中小学都采取了线上学习方式.为了解九年级学生网上学习的效果,甲、乙两个学校同时参加了一次相同的网上测试,记录成绩(百分制).分别从甲、乙两所学校随机抽取了20名学生的测试成绩,数据如下(百分制):
甲:63 70 95 84 75 82 78 78 86 96
92 100 52 89 88 84 84 92 90 84
乙:75 95 85 93 85 92 84 89 96 98
46 86 77 100 100 68 50 85 78 69
整理上面的数据,得到表格如下:
测试成绩(分) |
|
|
|
|
|
甲 | 1 | 2 | 3 | 9 | 5 |
乙 | 2 | 2 | 3 | 6 | 7 |
样本数据的平均数、中位数、众数如下表所示:
统计量 | 平均数 | 中位数 | 众数 |
甲 | 83.1 |
| 84 |
乙 | 82.4 | 85.5 |
|
根据以上信息,解答下列问题:
(1)表中的![]() ,
,![]() ;
;
(2)若甲学校共有500名学生,请用样本中的数据估计甲学校共有多少人的测试成绩达到优秀(规定:测试成绩![]() 分为优秀);
分为优秀);
(3)根据以上数据推断一所你认为成绩较好的学校,并说明理由.(至少从两个不同的角度结合数据说明推断的合理性)
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】在探究锐角三角函数的意义的学习过程中,小亮发现:“如图1,在![]() 中,
中,![]() ,可探究得到
,可探究得到![]() ”
”
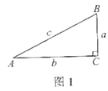
(1)请你利用图1探究说明小亮的说法是否正确;
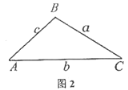
(2)小丽猜想“如果在钝角三角形中,两个锐角正弦值与它们所对边的边长之间也有一定的关系“在图2的钝角![]() 中,
中,![]() 是钝角,请你利用图2帮小丽探究
是钝角,请你利用图2帮小丽探究![]() 与
与![]() 之间的关系,并写出探究过程.
之间的关系,并写出探究过程.
(3)在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() 之间存在什么关系,请你探究并直接写出结论.
之间存在什么关系,请你探究并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=6,AD=10,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(x),当P,E,B三点在同一直线上时对应t的值为 .
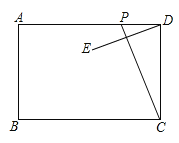
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
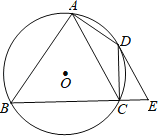
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣![]() x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
x+2的图象,绕x轴上一点P(m,0)旋转180°,所得的图象经过(0.﹣1),则m的值为( )
A.﹣2B.﹣1C.1D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和哥哥小明分别从家和图书馆同时出发,沿同一条路相向而行,小丽开始跑步,遇到哥哥后改为步行,到达图书馆恰好用35分钟,小明匀速骑自行车直接回家,骑行10分钟后遇到了妹妺,再继续骑行5分钟,到家两人距离家的路程y(m)与各自离开出发的时间x(min)之间的函数图象如图所示:
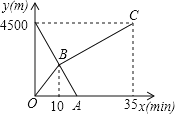
(1)求两人相遇时小明离家的距离;
(2)求小丽离距离图书馆500m时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
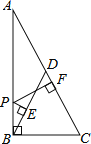
【题目】如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
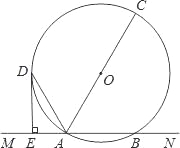
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com