【题目】如图，菱形ABCD中，E、F分别为BC、CD上的点，△AEF的三边长和菱形边长相等，求∠BAD的大小。
【答案】100°
【解析】
【试题分析】根据等边三角形△AEF得出，∠EAF=60°；根据△AEF的三边长和菱形边长相等，得出AB=AE，AF=AD；根据等边对等角，得出∠B=∠AEB，∠D=∠AFD；根据平行四边形的邻角互补，得出方程180°-2x+180°-2x+60°=180°-x，求解即可.
【试题解析】
∵△AEF的边长与菱形ABCD的边长相等，
∴△AEF是等边三角形，∠B+∠BAD=180°，AB=AE，AF=AD，
∴∠EAF=60°，∠B=∠AEB，∠D=∠AFD，
设∠B=x，则∠BAD=180°-x，
∠BAE=∠DAF=180°-2x，
即180°-2x+180°-2x+60°=180°-x，
解得：x=80°，
∴∠BAD=180°-80°=100°
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，边长为1的正方形OA1B1C的对角线 A1C和OB1交于点M1；以M1A1为对角线作第二个正方形A2A1B2M1，对角线A1M1和A2B2交于点M2；以M2A1为对角线作第三个正方形A3A1B3M2，对角线A1M2和A3B3交于点M3；……依此类推，这样作的第n 个正方形对角线交点Mn的坐标为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市为鼓励市民节约用水，特制定如下的收费标准：若每月每户用水不超过10立方米，则按3元/立方米的水价收费，并加收0.2元/立方米的污水处理费；若超过10立方米，则超过的部分按4元/立方米的水价收费，污水处理费不变．
（1）若小华家5月份的用水量为8立方米，那么小华家5月份的水费为_______元；
（2）若小华家6月份的用水量为15立方米，那么小华家6月份的水费为_______元；
（3）若小华家某个月的用水量为a（a＞10）立方米，求小华家这个月的水费（用含a的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚，数学中也存在着神奇的“黑洞数”现象：
(1)请你用不同的三个数再试试，你发现了什么“神奇”的现象？
(2)请用所学过的知识现象解释一下(1)中的发现．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线
平行于直线EC，且直线与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线上， 则DF的长为_____
查看答案和解析>>
科目：初中数学 来源： 题型：
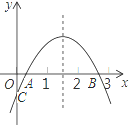
【题目】二次函数y＝ax2＋bx＋c（a≠0）的大致图象如图所示（1＜x＝h＜2，0＜xA＜1），下列结论：① 2a＋b＞0；② abc＜0；③ 若OC＝2OA，则2b－ac = 4；④ 3a﹣c＜0，其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB=4，∠BCD=120°，求四边形AODE的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC与Rt△ABD中，
，
，AC、BD相交于点G，过点A作
交CB的延长线于点E，过点B作
交DA的延长线于点F，AE、BF相交于点H．
（1）证明：ΔABD≌△BAC．
（2）证明：四边形AHBG是菱形．
（3）若AB=BC，证明四边形AHBG是正方形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
