
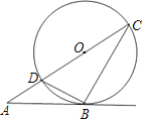
【题目】如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.
(1)求证:AB是⊙O的切线;
(2)若AB=4cm,AD=2cm,求tanA的值和DB的长.
【答案】(1)证明见解析;(2)tanA=![]() ;DB的长为
;DB的长为![]() .
.
【解析】
(1)连结OB,由等腰三角形的性质和圆周角定理证出∠CDB+∠C=90°,再由已知条件得出∠OBD+∠ABD=90°,得出∠OBA=90°即可;
(2)设半径为r,则OA=x+2,在Rt△AOB中,根据勾股定理得出方程,解方程求出半径,由三角函数求出得出tanA=![]() =
=![]() ,证明△ADB∽△ACB,得出
,证明△ADB∽△ACB,得出![]() =
=![]() ,设DB=x,则BC=2x,由勾股定理得出方程,解方程即可.
,设DB=x,则BC=2x,由勾股定理得出方程,解方程即可.
(1)证明:连结OB,如图所示:
∵OB=OD,
∴∠ODB=∠OBD,
∵DC是⊙O的直径,
∴∠DBC=90°,
∴∠CDB+∠C=90°,
∵∠ABD=∠C,
∴∠OBD+∠ABD=90°,
即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;

(2)解:设半径为r,则OA=x+2,
在Rt△AOB中,根据勾股定理得:x2+42=(x+2)2,
解得:r=3,
∴tanA=![]() =
=![]() ,
,
∵∠A=∠A,∠ABD=∠C,
∴△ADB∽△ACB,
∴![]() =
=![]() =
=![]() ,
,
设DB=x,则BC=2x,
∵CD=6,
∴由勾股定理得:x2+(2x)2=62,
解得:x=![]() ,
,
即DB的长为![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
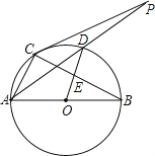
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.三角形ABC的三个顶点均在格点上,以点A为圆心的弧EF与BC相切于格点D,分别交AB,AC于点E,F.
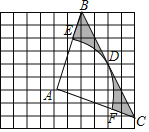
(1)直接写出三角形ABC边长AB= ;AC= ;BC= .
(2)求图中由线段EB,BC,CF及弧FE所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
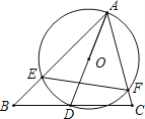
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为______.
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
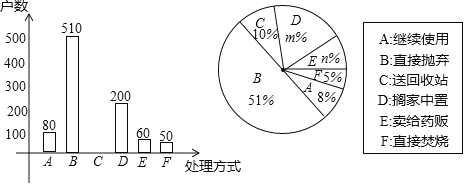
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
①m= ,n= ;
②补全条形统计图;
③扇形统计图中扇形C的圆心角度数是 ;
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论中错误的是( )
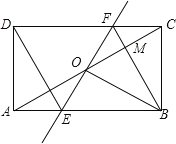
A.FB垂直平分OCB.DE=EF
C.S△AOE:S△BCM=3:2D.△EOB≌△CMB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度,2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2013年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2013年底共建设了多少万平方米廉租房.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com