
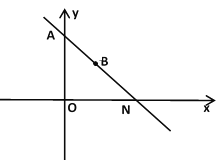
【题目】若直线y=kx+b过A(0,2)和点B(1,1),与x轴交于点N.
(1)直线的表达式为_________.
(2)在直线AB上有一点M(0.5,a),点Q是x轴上一个动点,若直线MQ把△AON的面积分成1:4两部分,求Q坐标.
【答案】(1)![]() (2)(
(2)(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)已知直线![]() 过A(0,2)和点B(1,1)两点,则可把两点坐标带入直线方程,求出k和b,再次代入得到直线的表达式.
过A(0,2)和点B(1,1)两点,则可把两点坐标带入直线方程,求出k和b,再次代入得到直线的表达式.
(2)先根据方程求出点M、N的坐标,再在ON之间标出点Q(x,0),连接MQ. 因为直线MQ把△AON的面积分成1:4两部分,所以△MQN与△AON的面积之比为1:5,然后写出方程,求x,即可知道Q点的坐标.
(1)分别把![]() 、
、![]() 与
与![]() 、
、![]() 带入直线方程
带入直线方程![]() 中,得到方程组
中,得到方程组![]() 解得
解得![]() ,则直线方程的表达式为
,则直线方程的表达式为![]() .
.
(2)①根据表达式![]() 得到N(2,0)和M(0.5,1.5),
得到N(2,0)和M(0.5,1.5),![]() ,.设 Q(x,0),则
,.设 Q(x,0),则![]() ,连接MQ,作MP垂直于x轴(MP是△MQN的高),如图所示:
,连接MQ,作MP垂直于x轴(MP是△MQN的高),如图所示:

则![]() .因为直线MQ把△AON的面积分成1:4两部分,所以△MQN与△AON的面积之比为1:5.
.因为直线MQ把△AON的面积分成1:4两部分,所以△MQN与△AON的面积之比为1:5.
![]() ,
,![]()
 ,解得
,解得![]() ,则Q(
,则Q(![]() ,0)
,0)
②如图所示,设 Q(a,0),C(0,c),则AC=2-c,作DM垂直于AC,则MD为三角形ACM的高.由①知 ,解得c=
,解得c=![]() .
.
设QM的解析式为y=kx+b,代入C(0,![]() ),M(0.5,1.5),则直线QM的解析式为:
),M(0.5,1.5),则直线QM的解析式为:![]()
求a的值,则令y=0,得a=![]() ,则Q(
,则Q(![]() ,0)
,0)



科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 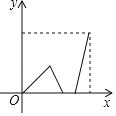
C.  D.
D. 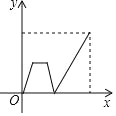
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF.

(1)你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角.
(2)试探索BE和CF有什么数量关系和位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校360名学生参加植树活动,要求每人植树3~6棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵.根据各类型对应的人数绘制了扇形统计图(如图1)和尚未完成的条形统计图(如图2).请解答下列问题:


(1)将条形统计图补充完整;
(2)这20名学生每人植树量的众数为________棵,中位数为________棵;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
第一步:求平均数的公式是![]() ;
;
第二步:在该问题中,n=4,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
第三步:![]() .
.
①小宇的分析是不正确的,他错在第几步?
请你帮他计算出正确的平均数,并估计这360名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 A(-2,0),B(0,m)两点,且线段AB= 2 ![]() ,以 AB 为边在第二象限内作正方形 ABCD。
,以 AB 为边在第二象限内作正方形 ABCD。

(1)求点 B 的坐标
(2)在 x 轴上是否存在点 Q,使△QAB 是以 AB 为腰的等腰三角形?若存在,请直接写出点 Q 的坐标,若不存在,请说明理由;
(3)如果在坐标平面内有一点 P(a,3),使得△ABP 的面积与正方形 ABCD 的面 积相等,求 a 的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com