
【题目】在圆O中,C是弦AB上的一点,联结OC并延长,交劣弧AB于点D,联结AO、BO、
AD、BD.已知圆O的半径长为5,弦AB的长为8.
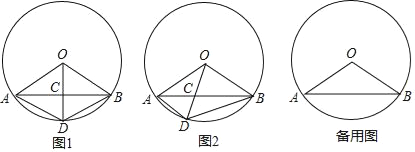
(1)如图1,当点D是弧AB的中点时,求CD的长;
(2)如图2,设AC=x,![]() =y,求y关于x的函数解析式并写出定义域;
=y,求y关于x的函数解析式并写出定义域;
(3)若四边形AOBD是梯形,求AD的长.
【答案】(1)2;(2)y=![]() (0<x<8);(3)AD=
(0<x<8);(3)AD=![]() 或6.
或6.
【解析】
(1)根据垂径定理和勾股定理可求出OC的长.
(2)分别作OH⊥AB,DG⊥AB,用含x的代数式表示△ACO和△BOD的面积,便可得出函数解析式.
(3)分OB∥AD和OA∥BD两种情况讨论.
解:(1)∵OD过圆心,点D是弧AB的中点,AB=8,
∴OD⊥AB,AC=![]() AB=4,
AB=4,
在Rt△AOC中,∵∠ACO=90°,AO=5,
∴CO=![]() =3,
=3,
∴OD=5,
∴CD=OD﹣OC=2;
(2)如图2,过点O作OH⊥AB,垂足为点H,
则由(1)可得AH=4,OH=3,
∵AC=x,
∴CH=|x﹣4|,
在Rt△HOC中,∵∠CHO=90°,AO=5,
∴CO=![]() =
=![]() =
=![]() ,
,
∴CD=OD﹣OC=5﹣![]() ,
,
过点DG⊥AB于G,
∵OH⊥AB,
∴DG∥OH,
∴△OCH∽△DCG,
∴![]() ,
,
∴DG=![]() =
=![]() ,
,
∴S△ACO=![]() AC×OH=
AC×OH=![]() x×3=
x×3=![]() x,
x,
S△BOD=![]() BC(OH+DG)=
BC(OH+DG)=![]() (8﹣x)×(3+
(8﹣x)×(3+![]() )=
)=![]() (8﹣x)×
(8﹣x)×![]()
∴y=![]() =
= =
=![]() (0<x<8)
(0<x<8)
(3)①当OB∥AD时,如图3,
过点A作AE⊥OB交BO延长线于点E,过点O作OF⊥AD,垂足为点F,
则OF=AE,
∴S=![]() ABOH=
ABOH=![]() OBAE,
OBAE,
AE=![]() =
=![]() =OF,
=OF,
在Rt△AOF中,∠AFO=90°,AO=5,
∴AF=![]() =
=![]()
∵OF过圆心,OF⊥AD,
∴AD=2AF=![]() .
.
②当OA∥BD时,如图4,过点B作BM⊥OA交AO延长线于点M,过点D作DG⊥AO,垂足为点G,
则由①的方法可得DG=BM=![]() ,
,
在Rt△GOD中,∠DGO=90°,DO=5,
∴GO=![]() =
=![]() ,AG=AO﹣GO=
,AG=AO﹣GO=![]() ,
,
在Rt△GAD中,∠DGA=90°,
∴AD=![]() =6
=6
综上得AD=![]() 或6.
或6.



故答案为:(1)2;(2)y=![]() (0<x<8);(3)AD=
(0<x<8);(3)AD=![]() 或6.
或6.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动.为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.
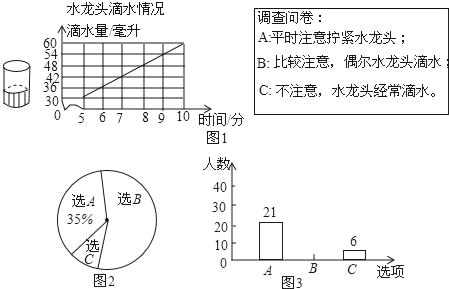
经结合图2和图3回答下列问题:
(1)参加问卷调查的学生人数为 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式.
(4)为了维持生命,每人每天需要约2400毫升水,该校选C的学生因没有拧紧水龙头,2小时浪费的水可维持多少人一天的生命需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:

其中有三天的个数墨汁覆盖了,但小强己经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
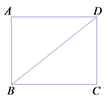
【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的
轴的
正半轴上,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 的坐标为
的坐标为![]() .
.

![]() 求
求![]() 的值.
的值.
![]() 若将菱形
若将菱形![]() 向右平移,使点
向右平移,使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,求菱形
的图象上,求菱形![]() 平移的距离.
平移的距离.
![]() 怎样平移可以使点
怎样平移可以使点![]() 、
、![]() 同时落在第一象限的曲线上?
同时落在第一象限的曲线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com