
【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗1L的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示: 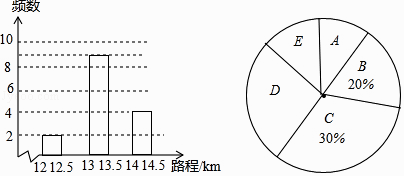
(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
(3)若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油1L的情况下可以行驶13km以上?
【答案】
(1)解:进行该试验的车辆数为:9÷30%=30(辆)
(2)解:B:20%×30=6(辆),
D:30﹣2﹣6﹣9﹣4=9(辆),
补全频数分布直方图如下:

(3)解:900× ![]() =660(辆),
=660(辆),
答:该市约有660辆该型号的汽车,在耗油1L的情况下可以行驶13km以上
【解析】(1)根据C所占的百分比以及频数,即可得到进行该试验的车辆数;(2)根据B的百分比,计算得到B的频数,进而得到D的频数,据此补全频数分布直方图;(3)根据C,D,E所占的百分比之和乘上该市这种型号的汽车的总数,即可得到结果.
【考点精析】关于本题考查的频数分布直方图和扇形统计图,需要了解特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能得出正确答案.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】百货商店销售某种冰箱,每台进价2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台。(销售利润=销售价—进价)
(1)如果设每台冰箱降价x元,那么每台冰箱的销售利润为 元,平均每天可销售冰箱 台;(用含x的代数式表示)
(2)商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆岗中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图. 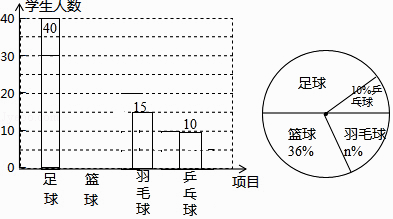
(1)m= , n=;
(2)请补全图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球;
(4)在抽查的m名学生中,喜爱乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作
如图1,在矩形纸片ABCD中,AB>AD.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.

问题解决
(1) 如图2,说明四边形AEFD是正方形;
(2) 如图4,判断NF与ND′的数量关系,并说明理由;
探索发现
(3)图4中MH与AM之间满足MH=nAM,请求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角三角形的三边长分别为a、b、c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形。那么,这四个图形中,其面积![]() 满足
满足![]() 的个数是( )
的个数是( )
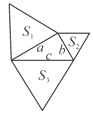
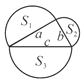
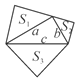

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校派相同人数的优秀学生,参加县教育局举办的中小学生美文诵读决赛。比赛结束后,发现学生成绩分别是7分、8分、9分或10分(满分10分),核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料,请你回答下列问题:
甲校成绩统计表 | ||||
成绩 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 | |
(1)在图①中,“7分”所在扇形的圆心角等于_______
(2)求图②中,“8分”的人数,并请你将该统计图补充完整。


(3)经计算,乙校学生成绩的平均数是8.3分,中位数是8分。请你计算甲校学生成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好?
(4)如果教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件正确的是( )
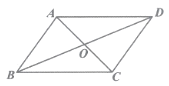
A. AB=AD B. AC=BD C. ∠ABC=90° D. ∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设,如图所示:①黑色瓷砖区域Ⅰ:位于四个角的边长相同的小正方形及宽度相等的回字型边框(阴影部分),②白色瓷砖区域Ⅱ:四个全等的长方形及客厅中心的正方形(空白部分).设四个角上的小正方形的边长为x(m).

(1)当x=0.8时,若客厅中心的正方形瓷砖铺设的面积为16m2,求回字型黑色边框的宽度;
(2)若客厅中心的正方形边长为4m,白色瓷砖区域Ⅱ的总面积为26m2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,当顶角A的大小确定时,它的对边BC与邻边(腰AB或AC)的比值确定,记为f(A),易得f(60°)=1.若α是等腰三角形的顶角,则f(α)的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com