
【题目】如图,在△ABC中,∠ABC=90°,AB=AC,点D在边AC上,将△ABD绕点B顺时针旋转得到△CBE,连接ED并延长交BA的延长线于点F.
(1)求证:∠CDE=∠ABD;
(2)探究线段AD,CD,BE之间的数量关系,并说明理由;
(3)若AD=1,CD=3,求线段EF的长.

【答案】(1)(2)见解析;(3)![]() .
.
【解析】
(1)先判断出△ABD≌△CBE,进而判断出∠ABD=∠CDE;
(2)先判断出△DCE是直角三角形,进而得出DE2=BD2+BE2=2BE2,即可得出结论;
(3)先利用勾股定理求出DE,再判断出△FAD∽△FDB,得出FD=![]() FA,最后用勾股定理求出FA即可得出结论.
FA,最后用勾股定理求出FA即可得出结论.
(1)证明:∵∠ABC=90°,AB=BC
∴∠BAC=∠ACB=45°,
∵△ABD绕点B顺时针旋转得到△CBE
∴△ABD≌△CBE,∠DBE=∠ABC=90°,
∴BD=BE,∠BCE=∠BAC=45°.
∴∠BDE=∠BED=45°.
∵∠BDC=∠BAD+∠ABD=∠ABD+45°,∠BDC=∠BDE+∠CDE=∠CDE+45°,
∴∠ABD=∠CDE.
(2)∵∠ACB=45°,∠BCE=45°,
∴∠DCE=∠ACB+∠BCE=90°.
∴CD2+CE2=DE2,
∵BD=BE,∠DBE=90°,
∴DE2=BD2+BE2=2BE2,
∵△ABD≌△CBE,
∴AD=CE.
∴AD2+CD2=2BE2,
(3)∵AD=1,CD=3,
∴AC=4,BD=BE=![]() =
=![]() .
.
∵∠DBE=90°,
∴DE=![]() =
=![]()
在Rt△ABC中,AB=ACsin∠ACB=2![]() .
.
∵∠ABD=∠CDE=∠ADF,∠F=∠F,
∴△FAD∽△FDB.
∴![]() ,即
,即![]()
∴FD=![]() FA,FD2=FAFB.
FA,FD2=FAFB.
∴(![]() FA)2=FA(FA+2
FA)2=FA(FA+2![]() ).解得FA=
).解得FA=![]() 或FA=0(舍去)
或FA=0(舍去)
∴FD=![]() FA=
FA=![]() .
.
∴EF=FD+DE= ![]()


科目:初中数学 来源: 题型:
【题目】(题文)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=2S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )

A. ①②③ B. ②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形 ABCD 的一条边 AD=8,将矩形 ABCD 折叠,使得顶点 B 落在 CD 边上的 P 点处.

(1)求证:△OCP∽△PDA;
(2)若△OCP 与△PDA 的面积比为 1:4,求边 AB 的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于数学课上需要用到科学计算器,班级决定集体购买,班长小明先去文具店购买了2个A型计算器和3个B型计算器,共花费90元;后又买了1个A型计算器和2个B型计算器,共花费55元(每次两种计算器的售价都不变)
(1)求A型计算器和B型计算器的售价分别是每个多少元?
(2)经统计,班内还需购买两种计算器共40个,设购买A型计算器t个,所需总费用w元,请求出w关于t的函数关系式;
(3)要求:B型计算器的数量不少于A型计数器的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(a,0),B(0,b)且a,b满足![]() ,
,
点P在线段AB上(含端点)的一点,连接OP。
(1)若AB=![]() ,且△OBP是以OB为腰长的等腰三角形,求BP的长;
,且△OBP是以OB为腰长的等腰三角形,求BP的长;
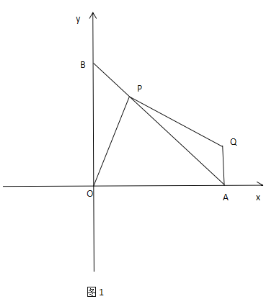
(2)如图1,过点A作AQ⊥x轴(Q在x轴上方),且满足∠OPQ=90°,求证:OP=PQ;
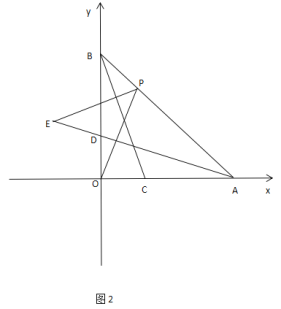
(3)如图2,C,D分别为OA,OB上的两点,且OC=OD,点P满足OP⊥AD,过点P作
PE⊥BC交AD的延长线于点E,试探究AE,OP,PE之间的数量关系,并给出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠BAD的平分线AE与BC边交于点E,点P是线段AE上一定点(其中PA>PE),过点P作AE的垂线与AD边交于点F(不与D重合).一直角三角形的直角顶点落在P点处,两直角边分别交AB边,AD边于点M,N.
(1)求证:△PAM≌△PFN;
(2)若PA=3,求AM+AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com