
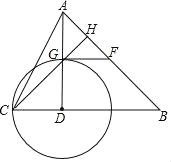
【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,tan∠ACD=2,以D为圆心,DC为半径作⊙D,交AD于点G,F是AB的中点,连接GF.
(1)求证:GF是⊙D的切线;
(2)连接CG并延长交AB于点H,若AH=2,求AC的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1)先证明G为AD的中点,可得GF为△ABD的中位线,则可证明∠AGF=90°;
(2)只要证明:△ADB,△CGD,△AGH都是等腰直角三角形,利用等腰三角形的性质即可解决问题;
(1)证明:∵tan∠ACD=![]() ,AD⊥BC,
,AD⊥BC,
∴AD=2CD=2GD,
∴G为AD的中点,
又∵F为AB的中点,
∴GF∥BD,
∵AD⊥BC,
∴∠AGF=90°,
∴GF是⊙D的切线;
(2)解:∵AD⊥BC,
∴∠ADB=90°,
∵∠B=45°,
∴△ADB是等腰直角三角形,
∴∠DAB=45°
∵GD=CD,∠GDC=90°,
∴△CGD是等腰直角三角形,
∴∠GCD=45°
∴∠AHC=90°,
∴△AGH是等腰直角三角形,
∵AH=2,
∴HG=2,AG=2![]() .
.
∴GD=2![]() ,
,
∴CG=4,
∴HC=6,
∴AC=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注,我市也在各个学校开展了传承经典的相关主题活动“戏曲进校园”.某校对此项活动的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
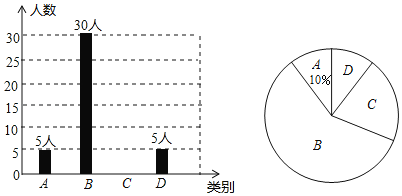
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是 人,扇形统计图中B部分所对应的扇形圆心角的度数为 ,并补全条形统计图;
(2)若该校共有学生1800人,请根据上述调查结果估计该校学生中A类有多少人;
(3)在A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树状图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
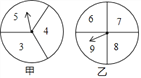
(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
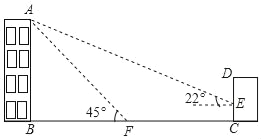
【题目】如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2米高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13米的距离(点B,F,C在同一条直线上),则AE之间的长为_____米.(结果精确到lm,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
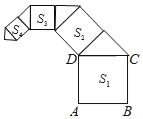
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2018的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
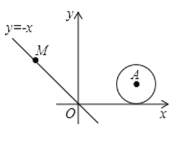
【题目】如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(2,1).直线OM是一次函数y=-x的图象.将直线OM沿x轴正方向平行移动.
(1)填空:直线OM与x轴所夹的锐角度数为 °;
(2)求出运动过程中⊙A与直线OM相切时的直线OM的函数关系式;(可直接用(1)中的结论)
(3)运动过程中,当⊙A与直线OM相交所得的弦对的圆心角为90°时,直线OM的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com