练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若关于x的方程x2+2x+k-1=0的一个根是0，则k=
     
    ．另外一个根为
     
    ．
    考点：根与系数的关系,一元二次方程的解
    专题：计算题
    分析：设方程的另外一个根为t，根据根与系数的关系得到0+t=-2，解得t=-2，然后再根据根与系数的关系得0×（-2）=k-1，再解一次方程即可得到k的值．
    解答： 解：设方程的另外一个根为t，
    根据题意得0+t=-2，解得t=-2，
    因为0×（-2）=k-1，
    所以k=1．
    故答案为1；-2．
    点评：本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
    b
    a
    ，x1x2=
    c
    a
    ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在正方形ABCD中，点P是对角线AC上一点，PE⊥AB，PF⊥BC，垂足分别是E、F．
    求证：DP=EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

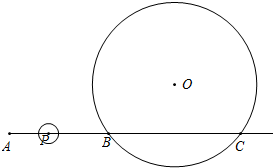    已知点C在射线AB上（点B在A、C之间），AB=12cm，BC=16cm，有一半径为10cm的⊙O过B、C两点，点P为射线AB上的一动点，且从点A出发，以1cm/秒的速度沿射线AB方向运动，设运动时间为t秒（t≥0），若以1cm为半径的⊙P与⊙O没有公共点，则t的取值范围为
     
    （结果可带根号表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    请你写出一个经过点（2，1）的一次函数解析式
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知x2+3x+1=0，试求x2+
    1
    x2
    与x4+
    1
    x4
    的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先阅读下面的内容，再解决问题，
    例题：若m2+2mn+2n2-6n+9=0，求m和n的值．
    解：∵m2+2mn+2n2-6n+9=0
    ∴m2+2mn+n2+n2-6n+9=0
    ∴（m+n）2+（n-3）2=0
    ∴m+n=0，n-3=0
    ∴m=-3，n=3
    问题：
    （1）若△ABC的三边长a，b，c都是正整数，且满足a2+b2-6a-6b+18+|3-c|=0，请问△ABC是什么形状？
    （2）若x2+4y2-2xy+12y+12=0，求xy的值．
    （3）已知a，b，c是△ABC的三边长，满足a2+b2=12a+8b-52，且△ABC是等腰三角形，求c．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简再求值：
    a-2
    a+3
    ÷
    a2-4
    2a+6
    -
    5
    a+2
    ．其中a=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

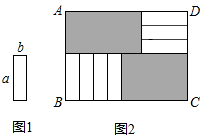    五张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（　　）
    A、a=bB、a=2b
    C、a=3bD、a=4b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在代数式①
    2
    x-1
    ；②
    x+y
    5
    ；③
    1
    -a
    ；④
    x
    π
    中，属于分式的有（　　）
    A、①②B、①③
    C、①③④D、①②③④

    查看答案和解析>>

    同步练习册答案