
分析 (1)根据解一元二次方程常用的方法换元法降次的方法,运用了数学转化思想;
(2)运用换元法设6x2-7x=a,然后运用因式分解法求解就可以了.
解答 解:(1)在由原方程得到方程①的过程中,利用了换元法,达到了降次的目的,体现了转化的数学思想.
(2)设6x2-7x=a,由题意,得
a2-2a-3=0,
解得:a1=3,a2=-1,
当a=3时,
6x2-7x=3,
解得:x1=-$\frac{1}{3}$,x2=$\frac{3}{2}$;
当a=-1时,
6x2-7x=-1,
解得:x3=$\frac{1}{6}$,x4=1.
∴原方程的解为:x1=-$\frac{1}{3}$,x2=$\frac{3}{2}$,x3=$\frac{1}{6}$,x4=1.
点评 本题考查了运用换元法解一元二次方程,一元二次方程的解法,把6x2-7x看作一个整体是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
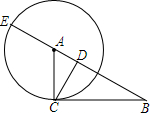 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com