
【题目】折纸是一项有趣的活动,在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念. 今天,就让我们带着数学的眼光来玩一玩折纸.
实践操作
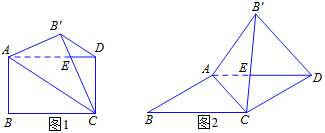
如图1,将矩形纸片ABCD沿对角线AC翻折,使点![]() 落在矩形ABCD所在平面内,
落在矩形ABCD所在平面内,![]() C和AD相交于点E,连接
C和AD相交于点E,连接![]() D.
D.
解决问题
(1)在图1中,①![]() D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
拓展应用
(3)在图2中,若∠B=30o,AB=![]() ,当A
,当A![]() ⊥AD时,BC的长度为_____.
⊥AD时,BC的长度为_____.
【答案】(1) BD′∥AC,菱形;(2)成立,理由见解析;(3)4或6或8或12.
【解析】
(1)①根据内错角相等两直线平行即可判断;
②根据菱形的判定方法即可解决问题;
(2)只要证明AE=EC,即可证明结论②成立;只要证明∠ADB′=∠DAC,即可推出B′D∥AC;
(3)先证得四边形ACB′D是等腰梯形,分四种情形分别讨论求解即可解决问题;
解:(1)①BD′∥AC.②将△AEC剪下后展开,得到的图形是菱形;
故答案为BD′∥AC,菱形;
(2)①选择②证明如下:
如图2,
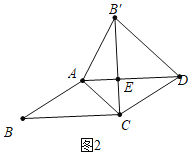
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵将△ABC沿AC翻折至△AB′C,
∴∠ACB′=∠ACB,
∴∠DAC=∠ACB′,
∴AE=CE,
∴△AEC是等腰三角形;
∴将△AEC剪下后展开,得到的图形四边相等,
∴将△AEC剪下后展开,得到的图形四边是菱形.
②选择①证明如下,
∵四边形ABCD是平行四边形,
∴AD=BC,
∵将△ABC沿AC翻折至△AB′C,
∵B′C=BC,
∴B′C=AD,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD
∴∠ADB′=∠DAC,
∴B′D∥AC.
(3)∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠B=30°,∴∠AB′C=∠CDA=30°,
∵△AB′D是直角三角形,
当∠B′AD=90°,AB>BC时,如图3中,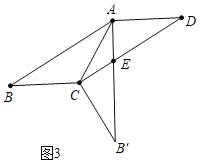
设∠ADB′=∠CB′D=y,
∴∠AB′D=y-30°,
解得y=60°,
∴∠AB′D=y-30°=30°,
∵AB′=AB=4![]()
![]()
∴BC=4,
当∠ADB′=90°,AB>BC时,如图4,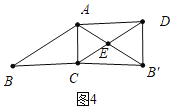
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠ADB′=90°,
∴四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵∠B=30°,AB=4![]()
![]()
当∠B′AD=90°,AB<BC时,如图5,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
![]()
∴∠AB′C=30°,
∴AE=4,BE′=2AE=8,
∴AE=EC=4,
∴CB′=12,
当∠AB′D=90°时,如图6,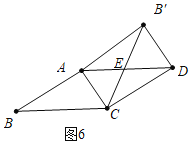
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是平行四边形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
![]()
![]()
∴已知当BC的长为4或6或8或12时,△AB′D是直角三角形.
故答案为:4或6或8或12;


科目:初中数学 来源: 题型:
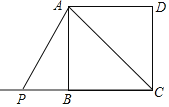
【题目】如图,在正方形ABCD中,点P在线段CB的延长线上,连接PA,将线段PA绕点P顺时针旋转90°,得到线段PE,连接CE,过点E作EF⊥BC于H,与对角线AC交于点F.
(1)请根据题意补全图形;
(2)求证:EH=FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,小明根据班上学生所报自选项目的情况绘制了统计图如下:
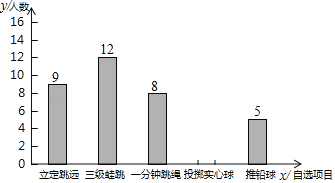
(1)补全条形统计图;
(2)若将各自选项的人数所占比例绘制成扇形统计图,求“三级蛙跳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取2名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=![]() AC
AC
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() . 点
. 点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,两点同时出发,速度都为每秒1个单位长度,当点
运动,两点同时出发,速度都为每秒1个单位长度,当点![]() 运动到
运动到![]() 时,两点都停止. 设运动时间为
时,两点都停止. 设运动时间为![]() 秒.
秒.
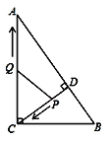
(1)求线段![]() 的长;
的长;
(2)当![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(3)是否存在某一时刻,使得![]() 分
分![]() 的面积为1:11?若存在,求出
的面积为1:11?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
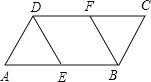
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com