
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() . 点
. 点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,两点同时出发,速度都为每秒1个单位长度,当点
运动,两点同时出发,速度都为每秒1个单位长度,当点![]() 运动到
运动到![]() 时,两点都停止. 设运动时间为
时,两点都停止. 设运动时间为![]() 秒.
秒.
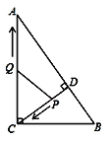
(1)求线段![]() 的长;
的长;
(2)当![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(3)是否存在某一时刻,使得![]() 分
分![]() 的面积为1:11?若存在,求出
的面积为1:11?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)![]() 为3秒或
为3秒或![]() 秒时,
秒时,![]() 是直角三角形;
是直角三角形;
(3)当![]() 时使得
时使得![]() 分
分![]() 的面积为1:11.
的面积为1:11.
【解析】
(1)利用勾股定理可求出AB长,再用等积法就可求出线段CD的长,
(2)先用t表示出DP,CQ,CP的长,再分PQ⊥CD与PQ⊥AC两种情况进行讨论;
(3)过点![]() 作
作![]() 于
于![]() ,通过三角形相似即可用t的代数式表示QE,从而可以求出
,通过三角形相似即可用t的代数式表示QE,从而可以求出![]() 和
和![]() ;利用
;利用![]() 分
分![]() 的面积为1:11,分两种情况讨论,①
的面积为1:11,分两种情况讨论,① ![]() ,②
,②![]() ,建立t的方程,解方程即可解决问题.
,建立t的方程,解方程即可解决问题.
解:(1)在![]() 中,根据勾股定理得,
中,根据勾股定理得,![]() ,
,
∵![]() ,
,
∴![]() ,
,
(2)由(1)知,![]() ,由运动知,
,由运动知,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,
∴①
当PQ⊥CD时,如图a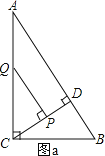
∴![]() ,
,
∴![]() ,
,
∴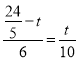 ,
,
∴![]()
②当PQ⊥AC,如图b.
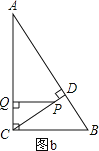
∴![]() ,
,
∴![]() ,
,
∴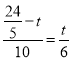
∴![]() ,
,
即:![]() 为3秒或
为3秒或![]() 秒时,
秒时,![]() 是直角三角形
是直角三角形
(3)假设存在,如图,
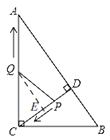
在![]() 中,根据勾股定理得,
中,根据勾股定理得,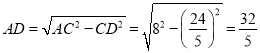 ,
,
过点![]() 作
作![]() 于
于![]() ,
,
∴,
∴![]() ,
,
∴![]() ,
,
∴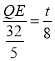 ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∵![]() 分
分![]() 的面积为1:11,
的面积为1:11,
∴①当![]() 时,
时,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
②当![]() 时,
时,
![]() ,
,
∴![]() ,
,
而![]() ,
,
此方程无解,即:此种情况不存在,
综上所述,当![]() 时使得
时使得![]() 分
分![]() 的面积为1:11.
的面积为1:11.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵![]() ≥0,
≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b=2
,(只有当a=b时,a+b=2![]() ).
).
即当a=b时,a+b取得最小值,且最小值为2![]() .
.
根据上述内容,回答下列问题:
问题1:若m>0,当m= 时,m+![]() 有最小值为 ;
有最小值为 ;
问题2:若函数y=a+![]() ,则当a= 时,函数y=a+
,则当a= 时,函数y=a+![]() 有最小值为 ;
有最小值为 ;
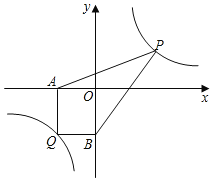
(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() 上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
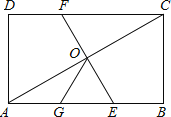
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,若点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)△OGE是等边三角形;(2)DC=3OG;(3)OG=![]() BC;(4)S△AOE=
BC;(4)S△AOE=![]() S矩形ABCD
S矩形ABCD
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸是一项有趣的活动,在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念. 今天,就让我们带着数学的眼光来玩一玩折纸.
实践操作
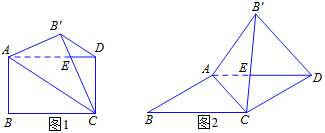
如图1,将矩形纸片ABCD沿对角线AC翻折,使点![]() 落在矩形ABCD所在平面内,
落在矩形ABCD所在平面内,![]() C和AD相交于点E,连接
C和AD相交于点E,连接![]() D.
D.
解决问题
(1)在图1中,①![]() D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
拓展应用
(3)在图2中,若∠B=30o,AB=![]() ,当A
,当A![]() ⊥AD时,BC的长度为_____.
⊥AD时,BC的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
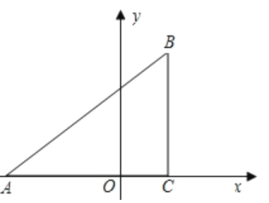
【题目】已知:如图,在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
(1)求过点![]() 的直线的函数表达式
的直线的函数表达式
(2)在![]() 轴上找一点
轴上找一点![]() ,连接
,连接![]() ,使得
,使得![]() 与
与![]() 相似(不包括全等),并求点
相似(不包括全等),并求点![]() 的坐标;
的坐标;
(3)在⑵的条件下,如![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,设
,设![]() ,问是否存在这样的
,问是否存在这样的![]() 使得
使得![]() 与
与![]() 相似,如果存在,请求出
相似,如果存在,请求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k+1)x+k2﹣2=0
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两个实数根为x1、x2,且满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,体育老师随机抽取了九年级甲、乙两班部分女生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和频数直方图,请你根据图表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)将频数直方图补充完整;
(3)如果该校九年级共有女生360人,估计仰卧起坐能够一分钟完成30次或30次以上的女学生有多少人?
(4)已知第一组有两名甲班学生,第四组中只有一名乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D为等腰Rt△ABC斜边AB的中点,DM⊥DN,DM,DN分别交BC,CA于点E,F.
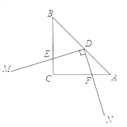
(1)当∠MDN绕点D转动时,求证:DE=DF.
(2)若AB=2,求四边形DECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
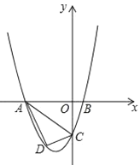
【题目】已知,如图抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.B的坐标为(1,0),且OC=4OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.B的坐标为(1,0),且OC=4OB.
(1)求点C坐标及抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求△ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com