
【题目】(阅读理解)对于任意正实数a、b,
∵![]() ≥0,
≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b=2
,(只有当a=b时,a+b=2![]() ).
).
即当a=b时,a+b取得最小值,且最小值为2![]() .
.
根据上述内容,回答下列问题:
问题1:若m>0,当m= 时,m+![]() 有最小值为 ;
有最小值为 ;
问题2:若函数y=a+![]() ,则当a= 时,函数y=a+
,则当a= 时,函数y=a+![]() 有最小值为 ;
有最小值为 ;
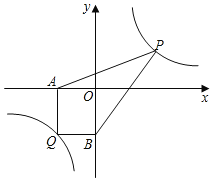
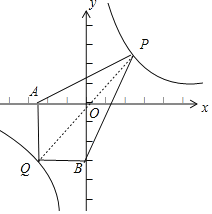
(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() 上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
【答案】问题1:2,4;问题2:4,7;【探索应用】四边形AQBP的面积的最小值为24.
【解析】
问题1:根据阅读材料的结论解答即可;
问题2:先变形y=![]() 得
得![]() ,再根据阅读材料的方法和结论即可求解;
,再根据阅读材料的方法和结论即可求解;
探索应用:先求出反比例函数的解析式,设出点P坐标,再用点P的横坐标表示出所求四边形面积,然后利用阅读材料提供的方法求解即可.
解:问题1:根据题意,当m=![]() 时,即m=±2,∵m>0,所以m=2,
时,即m=±2,∵m>0,所以m=2,
此时m+![]() 的最小值为2
的最小值为2![]() =4.
=4.
故答案为2、4;
问题2:∵a>1,∴![]() ,根据题意,得:
,根据题意,得:
y=![]() ,
,
当![]() 时,解得:
时,解得:![]() ,
,![]() (不合题意,舍去),∴
(不合题意,舍去),∴![]() ,
,
即当![]() 时,函数y=a+
时,函数y=a+![]() 有最小值7.
有最小值7.
故答案为4、7;
探索应用:
因为点Q(﹣3,﹣4)是双曲线y=![]() 上一点,所以k=12,所以双曲线为y=
上一点,所以k=12,所以双曲线为y=![]() .
.
连接PQ,设P(x,![]() ),
),
所以S四边形AQBP=![]() ×4(x+3)+
×4(x+3)+![]() ×3(
×3(![]() +4)=2x+
+4)=2x+![]() +12≥
+12≥![]() =12+12=24.
=12+12=24.
当![]() 时,即x=3时“=”成立.
时,即x=3时“=”成立.
所以四边形AQBP的面积的最小值为24.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】下列命题①相似三角形一定不是全等三角形;②相似三角形对应中线的等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O为△ABC内任意一点,OA、OB、OC的中点分别为![]() 、
、![]() 、
、![]() ,则有△
,则有△![]()
![]()
![]() ∽△ABC.其中正确的个数有( )
∽△ABC.其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
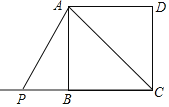
【题目】如图,在正方形ABCD中,点P在线段CB的延长线上,连接PA,将线段PA绕点P顺时针旋转90°,得到线段PE,连接CE,过点E作EF⊥BC于H,与对角线AC交于点F.
(1)请根据题意补全图形;
(2)求证:EH=FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
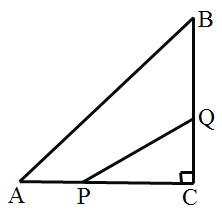
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 沿
沿![]() 向
向![]() 以
以![]() 的速度移动,到
的速度移动,到![]() 即停,点
即停,点![]() 从点
从点![]() 沿
沿![]() 向
向![]() 以
以![]() 的速度移动,到
的速度移动,到![]() 就停.
就停.
(1)若![]() 同时出发,经过几秒钟
同时出发,经过几秒钟![]() ;
;
(2)若点![]() 从
从![]() 点出发
点出发![]() 后点
后点![]() 从点
从点![]() 出发,再经过几秒
出发,再经过几秒![]() 与
与![]() 相似.
相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
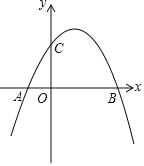
【题目】如图,抛物线 y=﹣![]() x2+
x2+![]() x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
(1)求 A,B,C的坐标;
(2)直线 l:y=﹣![]() x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,小明根据班上学生所报自选项目的情况绘制了统计图如下:
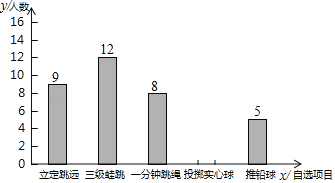
(1)补全条形统计图;
(2)若将各自选项的人数所占比例绘制成扇形统计图,求“三级蛙跳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取2名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() . 点
. 点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 运动,两点同时出发,速度都为每秒1个单位长度,当点
运动,两点同时出发,速度都为每秒1个单位长度,当点![]() 运动到
运动到![]() 时,两点都停止. 设运动时间为
时,两点都停止. 设运动时间为![]() 秒.
秒.
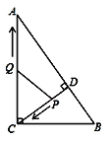
(1)求线段![]() 的长;
的长;
(2)当![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(3)是否存在某一时刻,使得![]() 分
分![]() 的面积为1:11?若存在,求出
的面积为1:11?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com