
【题目】下列命题①相似三角形一定不是全等三角形;②相似三角形对应中线的等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O为△ABC内任意一点,OA、OB、OC的中点分别为![]() 、
、![]() 、
、![]() ,则有△
,则有△![]()
![]()
![]() ∽△ABC.其中正确的个数有( )
∽△ABC.其中正确的个数有( )
A.1个B.2个C.3个D.4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,且
,且![]() 。
。
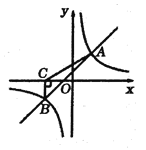
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() 的解集;
的解集;
(3)若![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线
(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线![]() 与直线
与直线![]() 有且只有一个交点;②若点
有且只有一个交点;②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为
;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为![]() ;④点A关于直线
;④点A关于直线![]() 的对称点为C,点D、E分别在x轴和y轴上,当
的对称点为C,点D、E分别在x轴和y轴上,当![]() 时,四边形BCDE周长的最小值为
时,四边形BCDE周长的最小值为![]() .其中正确判断的序号是__
.其中正确判断的序号是__
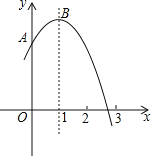
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形CAB中,CD⊥AB,垂足为D,圆E是△ACD的内切圆,切点分别为M,N,F,连接AE,BE.
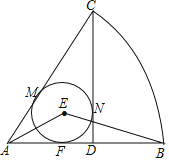
(1)求∠AEB的度数;
(2)若AD=DB,CD=3,求扇形CAB的弧长和圆E的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
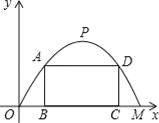
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵![]() ≥0,
≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b=2
,(只有当a=b时,a+b=2![]() ).
).
即当a=b时,a+b取得最小值,且最小值为2![]() .
.
根据上述内容,回答下列问题:
问题1:若m>0,当m= 时,m+![]() 有最小值为 ;
有最小值为 ;
问题2:若函数y=a+![]() ,则当a= 时,函数y=a+
,则当a= 时,函数y=a+![]() 有最小值为 ;
有最小值为 ;
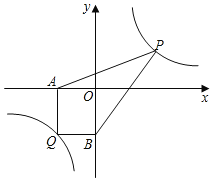
(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() 上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com